Alhazen facts for kids
Quick facts for kids
Alhazen
Ḥasan Ibn al-Haytham |
|
|---|---|
| ابن الهيثم | |
 |
|
| Born | c. 965 (c. 354 AH) Basra, Buyid Emirate
|
| Died | c. 1040 (c. 430 AH) (aged around 75) |
| Known for | Book of Optics, Doubts Concerning Ptolemy, Alhazen's problem, analysis, Catoptrics, horopter, intromission theory of visual perception, moon illusion, experimental science, scientific methodology, animal psychology |
| Scientific career | |
| Fields | physics, mathematics, astronomy |
| Influences | Aristotle, Euclid, Ptolemy, Galen, Banū Mūsā, Thābit ibn Qurra, Al-Kindi, Ibn Sahl, Abū Sahl al-Qūhī |
| Influenced | Omar Khayyam, Taqi ad-Din Muhammad ibn Ma'ruf, Kamāl al-Dīn al-Fārisī, Averroes, Al-Khazini, John Peckham, Vitello, Roger Bacon, Johannes Kepler |
Alhazen or Alhacen or ibn al-Haytham (965–1039) (Arabic: أبو علي الحسن بن الحسن بن الهيثم) was a pioneer of modern optics. Some have also described him as a "pioneer of the modern scientific method" and "first scientist", but others think this overstates his contribution. Alhazen's Risala fi’l-makan (Treatise on Place) discussed theories on the motion of a body. He maintained that a body moves perpetually unless an external force stops it or changes its direction of motion. He laid foundations for telescopic astronomy.
He was an Arab Muslim polymath who made contributions to the principles of optics, as well as to anatomy, engineering, mathematics, medicine, ophthalmology, philosophy, physics, psychology, Muslim theology, visual perception. He is sometimes called al-Basri (Arabic: البصري), after his birthplace in the city of Basra in Iraq (Mesopotamia).
Alhazen lived mainly in Cairo, Egypt, dying there at age 74. Over-confident about practical application of his mathematical knowledge, he thought he could regulate the floods of the Nile. When he was ordered by Al-Hakim bi-Amr Allah, the sixth ruler of the Fatimid caliphate, to carry out this operation, he realized he could not do it, and retired from engineering. Fearing for his life, he pretended to be mad, and was placed under house arrest. For the rest of his life he devoted himself entirely to his scientific work.
Contents
Biography
He was born in Basra, Iraq, then part of the Buwayhid Shia Muslim dynasty of Persia,[1] and he probably died in Cairo, Egypt.
Abū ‘Alī al-Hasan ibn al-Hasan ibn al-Haytham was one of the most eminent physicists, whose contributions to optics and the scientific method are outstanding. Known in the West as Alhacen or Alhazen, Ibn al-Haytham was born in 965 A. D. in Basrah, and was educated there and in Baghdad. One account of his career has him summoned to Egypt by the mercurial caliph Hakim to regulate the flooding of the Nile. After his field work made him aware of the impracticality of this scheme, and fearing the caliph's anger, he feigned madness. He was kept under house arrest until Hakim's death in 1021. During this time he wrote scores of important mathematical treatises. He later traveled to Spain and, during this period, he had ample time for his scientific pursuits, which included optics, mathematics, physics, medicine and development of scientific methods on each of which he has left several outstanding books.
He made a thorough examination of the passage of light through various media and discovered the laws of refraction. He also carried out the first experiments on the dispersion of light into its constituent colours. His book Kitab al-Manazir (Book of Optics) was translated into Latin in the Middle Ages, as also was his book dealing with the colours of sunset. He dealt at length with the theory of various physical phenomena such as shadows, eclipses, and the rainbow, and speculated on the physical nature of light. He is the first to describe accurately the various parts of the eye and give a scientific explanation of the process of vision. He also attempted to explain binocular vision and the apparent increase in size of the Sun and the Moon when near the horizon. He is known for the earliest use of the camera obscura. He contradicted Ptolemy's and Euclid's theory of vision that objects are seen by rays of light emanating from the eyes; according to him the rays originate in the object of vision and not in the eye. Through these extensive researches on optics, he has been considered as the father of modern optics.
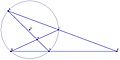
The Latin translation of his main work, Kitab al-Manazir, exerted a great influence upon Western science e.g. on the work of Roger Bacon who cites him by name and Kepler. It brought about a great progress in experimental methods. His research in catoptrics centered on spherical and parabolic mirrors and spherical aberration. He made the important observation that the ratio between the angle of incidence and refraction does not remain constant and investigated the magnifying power of a lens. His catoptrics contain the important problem known as "Alhazen's problem". It comprises drawing lines from two points in the plane of a circle meeting at a point on the circumference and making equal angles with the normal at that point. This leads to an equation of the fourth degree.
The list of his books runs to 200 or so, yet very few of the books have survived. Even his monumental treatise on optics survived only through its Latin translation. During the Middle Ages his books on cosmology were translated into Latin, Hebrew and other languages.
Ibn al-Haytham's work on optics is credited with contributing a new emphasis on experiment, drawing in part on the astronomical and optical work of Ptolemy. His influence on physical sciences in general, and optics in particular, has been held in high esteem and, in fact, it ushered in a new era in optical research, both in theory and practice.
Alhacen is featured on the obverse of the Iraqi 10,000 dinars banknote issued in 2003. The asteroid 59239 Alhazen was also named in his honour. And Iran's largest laser research facility, located in the Atomic Energy Organization of Iran headquarters in Tehran is named after Alhacen as well.
Major works
Alhacen was a pioneer in optics, astronomy, engineering, mathematics and physics. His contribution to mathematics and physics was also extensive. Alhacen taught that vision does not result from the emission of rays from the eye, and wrote on the refraction of light, especially on atmospheric refraction, for example, the cause of morning and evening twilight. He solved the problem of finding the point on a convex mirror at which a ray coming from one point is reflected to another point.
Alhacen's optical writings influenced many Western intellectuals such as Roger Bacon, John Pecham, Witelo, and Johannes Kepler.
Book of Optics
His seven volume treatise on optics, Kitab al-Manazir (Book of Optics) (written from 1015 to 1021), drastically transformed the ancient understanding of vision. In classical antiquity, there were two major theories on vision. The first theory, the emission theory, was supported by such thinkers as Euclid and Ptolemy, who believed that sight worked by the eye emitting rays of light. The second theory, the intromission theory, supported by Aristotle and his followers, had physical particles entering the eye. Alhacen argued on the basis of common observations (such as the eye being dazzled or even injured if we look at a very bright light) and logical arguments (such as how a ray could proceeding from the eyes reach the distant stars the instant after we open our eye) to maintain that we cannot see by rays being emitted from the eye nor through particles entering the eye. Alhacen instead developed a highly successful theory which explained the process of vision by rays of light proceeding to the eye from each point on an object, which he proved through the use of experimentation.
Optics was translated into Latin by an unknown scholar at the end of the 12th century or the beginning of the 13th century. It was printed by Friedrich Risner in 1572, with the title Opticae thesaurus: Alhazeni Arabis libri septem, nuncprimum editi; Eiusdem liber De Crepusculis et nubium ascensionibus [2]. Risner is also the author of the name variant "Alhazen", before him he was known in the west as Alhacen, which is correct transcription of the Arabic name. This work enjoyed a great reputation during the Middle Ages. Works by Alhacen on geometrical subjects were discovered in the Bibliothèque nationale in Paris in 1834 by E. A. Sedillot. Other manuscripts are preserved in the Bodleian Library at Oxford and in the library of Leiden.
In his work on optics, Alhacen described sight as the inference of distinct properties of two similar and dissimilar objects. The eye perceives the size, shape, transparency (color and light), position, and motion from cognitive distinction which is entirely different from perceiving by mere sensation the characteristics of the object. The faculty of the mind, for Alhacen, includes perceiving through judgement and inference of distinct properties of similar objects outline and structure. Alhacen continues this body of work by concluding that the discrimination performed by the faculty of judgment and inference is in addition to sensing the objects visible form and not by pure sensation alone. We recognize visible objects that we frequently see. Recognition of an object is not pure sensation because we do not recognize everything we see. Ultimately, recognition does not take place without remembering. Recognition is due to the inference because of our mental capacity to conclude what objects are. Alhacen uses our ability to recognize species and likening their characteristics to that of similar individuals to support recognition associated and processed by inference. Alhacen further concludes that we are processing visual stimuli in very short intervals which allows us to recognize and associate objects through inference but we do not need syllogism to recognize it. These premises are stored infinitely in our souls. Alhacen is also credited to have invented the camera obscura and pinhole camera.
Robert S. Elliot writes:
"Alhazen was one of the ablest students of optics of all times and published a seven-volume treatise on this subject which had great celebrity throughout the medieval period and strongly influenced Western thought, notably that of Roger Bacon and Kepler. This treatise discussed concave and convex mirrors in both cylindrical and spherical geometries, anticipated Fermat's law of least time, and considered refraction and the magnifying power of lenses. It contained a remarkably lucid description of the optical system of the eye, which study led Alhazen to the belief that light consists of rays which originate in the object seen, and not in the eye, a view contrary to that of Euclid and Ptolemy."
The foundations of telescopic astronomy can also be traced back to Ibn al-Haytham. His optical studies were influential in the later development of the telescope.
Treatise on Light
His Risala fi l-Daw’ (Treatise on Light) is a supplement to his Kitab al-Manazir (Book of Optics). The text contained further investigations on the properties of luminance and its radiant dispersion through various transparent and translucent media. He also carried out further observations, investigations and examinations on the anatomy of the eye, the camera obscura and pinhole camera, the illusions in visual perception, the meteorology of the rainbow and the density of the atmosphere, various celestial phenomena (including the eclipse, twilight, and moonlight), refraction, catoptrics, dioptrics, spherical and parabolic mirrors, and magnifying lenses.
Analysis and Synthesis
His contributions to number theory includes his work on perfect numbers. In his Analysis and Synthesis, Ibn al-Haytham was the first to realize that every even perfect number is of the form 2n−1(2n − 1) where 2n − 1 is prime, but he was not able to prove this result successfully (Euler later proved it in the 18th century).
Opuscula
In number theory, Ibn al-Haytham solved problems involving congruences using what is now called Wilson's theorem. In his Opuscula, Ibn al-Haytham considers the solution of a system of congruences, and gives two general methods of solution. His first method, the canonical method, involved Wilson's theorem, while his second method involved a version of the Chinese remainder theorem.
Doubts on Ptolemy
Ibn al-Haytham wrote a scathing critique of the physical reality of Ptolemy's astronomical system, noting the absurdity of relating actual physical motions to imaginary mathematical points, lines, and circles:
"Ptolemy assumed an arrangement that cannot exist, and the fact that this arrangement produces in his imagination the motions that belong to the planets does not free him from the error he committed in his assumed arrangement, for the existing motions of the planets cannot be the result of an arrangement that is impossible to exist."
Ibn al-Haytham argued that the equant introduced by Ptolemy failed to satisfy the Ptolemaic model's requirement of uniform circular motion. While he attempted to discover the physical reality behind Ptolemy's mathematical model, he developed the concept of a single celestial sphere for each component of Ptolemy's planetary motions. This work was eventually translated into Latin by the 14th century and subsequently had an important influence during the European Renaissance.
On the Configuration of the World
Despite his criticisms directed towards Ptolemy, Ibn al-Haytham continued to accept the physical reality of the geocentric model of the universe, presenting a detailed description of the physical structure of the celestial spheres in his On the Configuration of the World:
"The earth as a whole is a round sphere whose center is the center of the world. It is stationary in its [the world's] middle, fixed in it and not moving in any direction nor moving with any of the varieties of motion, but always at rest."
According to Giambattista della Porta, Alhacen was the first to give a correct explanation of the apparent increase in the size of the Moon and Sun when near Earth's horizon. (Ptolemy made earlier attempts at explaining it, according to Roger Bacon.)
Maqala fi'l-qarastun
The Maqala fi'l-qarastun is a treatise on centers of gravity. Little is currently known about the work, except for what is known through the later works of al-Khazini in the 12th century. In this treatise, Ibn al-Haytham formulated the theory that the heaviness of bodies vary with their distance from the center of the Earth.
Mizan al-Hikmah
In his book Mizan al-Hikmah, Ibn al-Haytham has discussed the density of the atmosphere and related it to altitude. He also studied atmospheric refraction. He discovered that the twilight only ceases or begins when the Sun is 19° below the horizon and attempted to measure the height of the atmosphere on that basis. He also discussed the theory of attraction between masses, and it seems that he was aware of the magnitude of acceleration due to gravity.
Treatise on Place
Ibn al-Haytham's Risala fi’l-makan (Treatise on Place) presents a critique of Aristotle's concept of place (topos). Aristotle's Physics stated that the place of something is the two-dimensional boundary of the containing body that is at rest and is in contact with what it contains. Ibn al-Haytham disagreed and demonstrated that place (al-makan) is the imagined three-dimensional void between the inner surfaces of the containing body. He showed that place was akin to space, foreshadowing Rene Descartes’ concept of place in the Extensio in the 17th century. Ibn al-Haytham also builds on the mathematical works of Euclid and Thabit ibn Qurra, and goes on to systemize infinitesimal calculus, conic sections, number theory, and analytic geometry after linking algebra to geometry. Ibn al-Haytham also studied the mechanics of the motion of a body and maintained that a body moves perpetually unless an external force stops it or changes its direction of motion. This was similar to the law of inertia later stated by Galileo Galilei in the 16th century and now known as Newton's first law of motion.
Other contributions
Yasmeen M. Faruqi writes:
"In seventeenth century Europe the problems formulated by Ibn al-Haytham (965-1041) became known as “Alhazen’s problem”. [...] Al-Haytham’s contributions to geometry and number theory went well beyond the Archimedean tradition. Al-Haytham also worked on analytical geometry and the beginnings of the link between algebra and geometry. Subsequently, this work led in pure mathematics to the harmonious fusion of algebra and geometry that was epitomised by Descartes in geometric analysis and by Newton in the calculus. Al-Haytham was a scientist who made major contributions to the fields of mathematics, physics and astronomy during the latter half of the tenth century."
Calculus
His work on catoptrics contains the important problem known as "Alhazen's problem". It comprises drawing lines from two points in the plane of a circle meeting at a point on the circumference and making equal angles with the normal at that point. This leads to an equation of the fourth degree. This eventually led Ibn al-Haytham to derive the earliest formula for the sum of the fourth powers, and using an early proof by mathematical induction, he developed a method for determining the general formula for the sum of any integral powers, which was fundamental to the development of infinitesimal and integral calculus.
Geometry
In mathematics, Ibn al-Haytham developed analytical geometry by establishing linkage between algebra and geometry. Ibn al-Haytham also discovered a formula for adding the first 100 natural numbers, which was later often attributed to Carl Friedrich Gauss. Ibn al-Haytham had used a geometric proof to prove the formula. His attempted proof of the parallel postulate was also similar to the Lambert quadrilateral and Playfair's axiom in the 18th century. In elementary geometry, Ibn al-Haytham attempted to solve the problem of squaring the circle using the area of lunes, but later gave up on the impossible task.
Hockney-Falco thesis
At a scientific conference in February 2007, Charles M. Falco speculated that Ibn al-Haytham did work on optics that may have influenced the use of optical aids by Renaissance artists. Falco said that his and David Hockney's examples of Renaissance art "demonstrate a continuum in the use of optics by artists from c. 1430, arguably initiated as a result of Ibn al-Haytham's influence, until today."
Images for kids
-
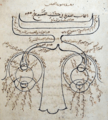
The structure of the human eye according to Ibn al-Haytham. Note the depiction of the optic chiasm. —Manuscript copy of his Kitāb al-Manāẓir (MS Fatih 3212, vol. 1, fol. 81b, Süleymaniye Mosque Library, Istanbul)
-
Cover page of the Latin translation of Kitāb al-Manāẓir
See also
 In Spanish: Alhacén para niños
In Spanish: Alhacén para niños