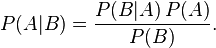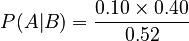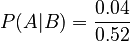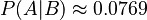Bayes' theorem Facts for Kids

Bayes' theorem is a super useful idea in probability theory that helps us understand how likely something is to happen, especially when we get new information. It's like updating your guess about something after you learn more facts. For example, you might want to know the chance of a certain event happening, given some clues you've found. This theorem is named after Thomas Bayes, a smart person from a long time ago, and it's also called Bayes' law or Bayes' rule.

How Bayes' Theorem Works
A Simple Example
- Calculating the Chance of Rain on Monday
- Using Bayes' Theorem
Why Bayes' Theorem Makes Sense
Related pages
Images for kids
See also

How Bayes' Theorem Works

Bayes' theorem uses a special formula to connect two different kinds of probabilities. It links the chance of something happening (let's call it 'A') when you already know something else has happened (let's call it 'B'), with the chance of 'B' happening when 'A' has occurred.

The main formula looks like this:

P(A|B) = \frac{P(B | A)\, P(A)}{P(B)}.

Let's break down what each part means:

P(A) is the starting chance of event A happening. We call this the "prior probability" because it's what you think before you get any new information about B.
P(A|B) is the chance of event A happening, given that event B has already happened. This is called the "posterior probability" because it's your updated chance after considering the new information from B.
P(B|A) is the chance of event B happening, given that event A has already happened. This is sometimes called the "likelihood."
P(B) is the starting chance of event B happening. It helps to make sure our final probability makes sense.

Sometimes, calculating P(B) can be tricky. A common way to find P(B) is by adding up the chances of B happening when A happens, and B happening when A doesn't happen. The formula for this is: $P(B) = P(B|A)P(A) + P(B|A^c)P(A^c)$ .

A Simple Example

Let's use an example to make this clearer. Imagine you want to predict the weather:

There's a 40% chance of rain on Sunday.
If it rains on Sunday, there's a 10% chance it will rain on Monday.
If it does NOT rain on Sunday, there's an 80% chance it will rain on Monday.

Let's define our events:

Event A: "Raining on Sunday"
Event B: "Raining on Monday"

Now, let's write down the probabilities we know:

P( A ) = 0.40 (40%) = Chance of rain on Sunday.
P( A` ) = 0.60 (60%) = Chance of NO rain on Sunday (since 1 - 0.40 = 0.60).
P( B | A ) = 0.10 (10%) = Chance of rain on Monday, if it rained on Sunday.
P( B` | A ) = 0.90 (90%) = Chance of NO rain on Monday, if it rained on Sunday.
P( B | A` ) = 0.80 (80%) = Chance of rain on Monday, if it did NOT rain on Sunday.
P( B` |A` ) = 0.20 (20%) = Chance of NO rain on Monday, if it did NOT rain on Sunday.

Calculating the Chance of Rain on Monday

First, let's figure out the overall chance of it raining on Monday (P(B)). It can rain on Monday in two ways: 1. It rains on Sunday AND then rains on Monday. 2. It does NOT rain on Sunday AND then rains on Monday.

So, we add these chances together:

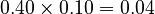
(Chance of rain on Sunday) multiplied by (Chance of rain on Monday given rain on Sunday) = Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 0.40 \times 0.10 = 0.04
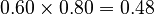
(Chance of no rain on Sunday) multiplied by (Chance of rain on Monday given no rain on Sunday) = Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 0.60 \times 0.80 = 0.48

Adding these up: 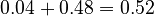Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 0.04 + 0.48 = 0.52 . So, P(B) = 0.52, meaning there's a 52% chance it will rain on Monday.

Using Bayes' Theorem

Now, here's where Bayes' theorem becomes really useful! What if we want to know the chance that it rained on Sunday, given that we know it rained on Monday? This is asking about an earlier event based on a later event.

We use the formula:

P(A|B) = \frac{P(B | A)\, P(A)}{P(B)}.

Let's plug in our numbers:

P(B|A) = 0.10 (Chance of rain on Monday if it rained on Sunday)
P(A) = 0.40 (Chance of rain on Sunday)
P(B) = 0.52 (Overall chance of rain on Monday, which we just calculated)

So, the calculation is:

Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): P(A|B) = \frac{0.10 \times 0.40}{0.52}

Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): P(A|B) = \frac{0.04}{0.52}

Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): P(A|B) \approx 0.0769

This means that if you know it rained on Monday, there was only about a 7.69% chance that it also rained on Sunday. This is much lower than the original 40% chance of rain on Sunday! Bayes' theorem helped us update our belief.

Why Bayes' Theorem Makes Sense

Think about it this way: We want to find the chance that it rained on Sunday, knowing it rained on Monday.

We know the total chance of rain on Monday is P(B).
We also know the chance of it raining on Sunday and raining on Monday. This is P(A) multiplied by P(B|A).

So, if we divide the chance of "raining on Sunday AND Monday" by the "total chance of raining on Monday," we get the chance of "raining on Sunday, given it rained on Monday."

Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): P(A|B) = \frac{\text{Chance of (A and B)}}{\text{Total Chance of B}} = \frac{P(B | A)\, P(A)}{P(B)}.

Another way to see this is that the chance of both A and B happening (P(A and B)) can be written in two ways:

P(A and B) = P(A) multiplied by P(B|A) (Chance of A, then B given A)
P(A and B) = P(B) multiplied by P(A|B) (Chance of B, then A given B)

Since both ways describe the same thing, they must be equal:

P(A)\, P(B|A) = P(B)\, P(A|B)

If you rearrange this equation to solve for P(A|B), you get Bayes' theorem! It's just a different way to look at how probabilities are connected.

Images for kids

A blue neon sign showing the simple statement of Bayes's theorem

Bayes' theorem facts for kids

Contents