De Morgan's laws facts for kids
De Morgan's laws are important rules in boolean algebra, which is a type of math used in computer science and logic. These laws help us understand how "NOT" statements affect "AND" and "OR" statements.
Imagine you have two statements, A and B.
The first law says:
- If you say "NOT (A AND B)", it's the same as saying "(NOT A) OR (NOT B)".
- In symbols, this looks like:
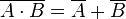
The second law says:
- If you say "NOT (A OR B)", it's the same as saying "(NOT A) AND (NOT B)".
- In symbols, this looks like:
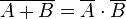
A simple way to remember these laws is "break the line, change the sign". This means if you have a "NOT" over a group (like the line over A and B), you can "break" that line over each part, but then you must "change" the "AND" to an "OR", or the "OR" to an "AND".
Understanding Truth Tables
Truth tables are like charts that show all possible outcomes for a logical statement. They help us prove that De Morgan's laws are correct. In these tables, '0' means "false" and '1' means "true".
First Law: NOT (A AND B)
This table shows that "NOT (A AND B)" gives the same result as "(NOT A) OR (NOT B)".
| INPUT | OUTPUT 1 | OUTPUT 2 | |
| A | B | NOT (A AND B) | (NOT A) OR (NOT B) |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
Second Law: NOT (A OR B)
This table shows that "NOT (A OR B)" gives the same result as "(NOT A) AND (NOT B)".
| INPUT | OUTPUT 1 | OUTPUT 2 | |
| A | B | NOT (A OR B) | (NOT A) AND (NOT B) |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 |
See also
Learn more in Spanish: Leyes de De Morgan para niños
