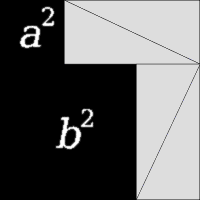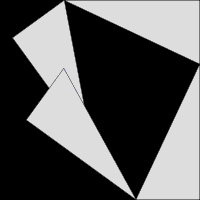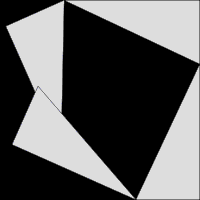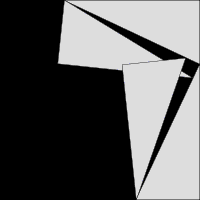
Image: Pythag anim
Description: Animation of a proof of Pythagoras' theorem, showing how by rearranging triangles the areas a2 + b2 and c2 can be shown to be the same. The area of the outer square never changes, and the total area of the four right triangles is the same at both the beginning and the end, therefore the black area at the beginning, a2 + b2, must equal the black area at the end, c2. The angle of the triangles is arbitrary, therefore this works as a general proof. To be more explicit... The situation at the start is: Area_of_the_Outer_Square - (4 x Area_of_a_Triangle) = a2 + b2 ...and the situation at the end is: Area_of_the_Outer_Square - (4 x Area_of_a_Triangle) = c2 The values on both left-hand sides of these two equations are exactly the same (only positions have changed) therefore the values on the right-hand sides must also be exactly the same: a2 + b2 = c2.
Title: Pythag anim
Credit: Own work
Author: JohnBlackburne
Usage Terms: Creative Commons Attribution-Share Alike 3.0
License: CC BY-SA 3.0
License Link: http://creativecommons.org/licenses/by-sa/3.0
Attribution Required?: Yes
Image usage
The following page links to this image: