Image: Triadic harmonic entropy

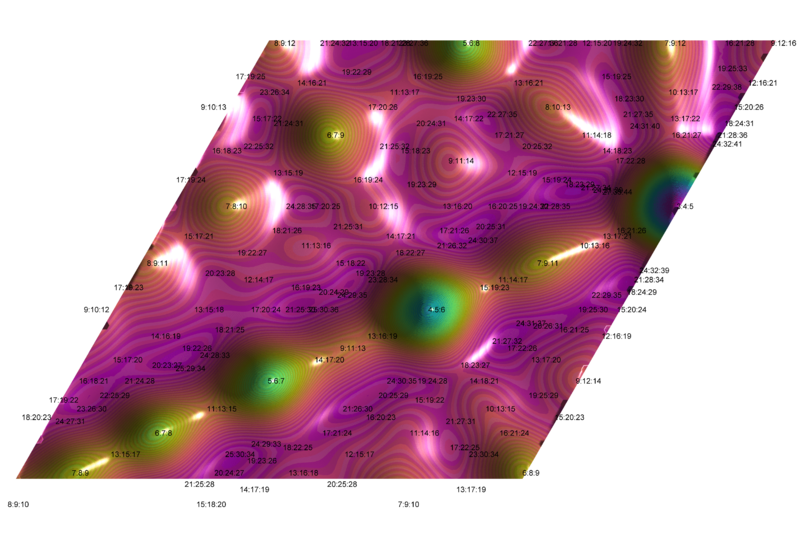
Description: Triadic harmonic entropy for triads with lower interval and upper interval each ranging from 200 (augmented minor third: E) to 500 (augmented major third: E) cents. Lower interval plotted horizontally, upper interval diagonally and to the right, graph shows most consonant triads as the highest points. Harmonic entropy theory is intended to model one of the components of dissonance as a measure of the uncertainty of the virtual pitch ("missing fundamental") evoked by a set of two or more pitches. So for instance, in this plot, notice how the harmonic major triad 4:5:6 is a clear prominent peak. The usual 5 limit harmonic minor triad 10:12:15 (i.e. 1/4 : 1/5 : 1/6) is less prominent, as expected; indeed though it looks like a hill from most directions; it turns out to be a small hillock on the slopes of the 6:7:9 mountain (septimal minor triad). Formula by Paul Erlich; calculations by Steve Martin; graphic by Paul Erlich For details of how harmonic entropy is calculated see Harmonic Entropy from Bill Sethares' book Tuning Timbre Spectrum Scale and described in more detail here and here For example, compare 4:5:6, 6:7:9, and 10:12:15.
Title: Triadic harmonic entropy
Credit: Author of graphic gave it to me to upload
Author: Paul Erlich
Usage Terms: Creative Commons Attribution-Share Alike 3.0 us
License: CC BY-SA 3.0 us
License Link: https://creativecommons.org/licenses/by-sa/3.0/us/deed.en
Attribution Required?: Yes