Optimal solutions for Rubik's Cube facts for kids
Optimal solutions for the Rubik's Cube are the shortest ways to solve a scrambled cube. Imagine you have a Rubik's Cube that's all mixed up. An "optimal solution" means finding the fewest possible moves to get it back to its solved state.
There are two main ways to count these moves:
- Quarter Turn Metric (QTM): Each turn of a face, even a half-turn (180 degrees), counts as two moves. So, a 90-degree turn is one move, and a 180-degree turn is two moves.
- Face Turn Metric (FTM): Each turn of a face, whether it's 90 degrees or 180 degrees, counts as just one move. This is also sometimes called the "Half Turn Metric" (HTM).
Scientists and mathematicians have found that the fewest moves needed to solve *any* Rubik's Cube are:
- 20 moves using the Face Turn Metric (FTM).
- 26 moves using the Quarter Turn Metric (QTM).
These numbers are known as "God's Number" for the Rubik's Cube, because they represent the absolute minimum number of moves needed from any starting position.
Contents
How We Talk About Moves
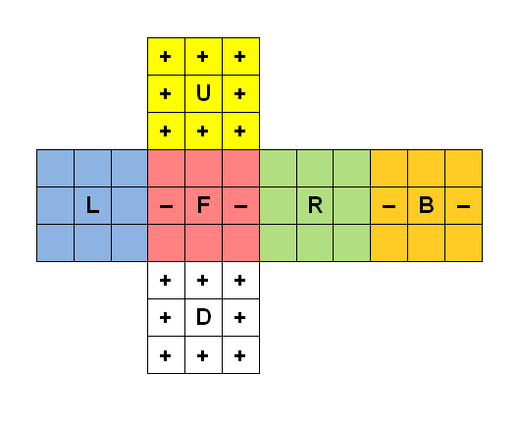
To describe how to turn the cube, people use a special language called "Singmaster notation." It's like a secret code for cube solvers!
- L, R, F, B, U, D: These letters mean you turn the Left, Right, Front, Back, Up, or Down face 90 degrees clockwise.
- 2: If you see a "2" after a letter (like F2), it means you turn that face 180 degrees (a half-turn).
- ': If you see a prime symbol (like F'), it means you turn that face 90 degrees counter-clockwise (the opposite direction).
So, F means turn the front face clockwise. F2 means turn the front face 180 degrees. F' means turn the front face counter-clockwise.
How Many Moves Are Needed?
For a long time, people wondered what the absolute fewest moves were to solve any Rubik's Cube.
Finding the Smallest Number of Moves
Scientists used math to prove that some cube positions would need at least 18 moves to solve. They did this by counting all possible cube positions and comparing them to how many positions you could reach with fewer than 18 moves.
One famous hard position is called the superflip. In this state, all the corner pieces are in the right spot, but all the edge pieces are flipped incorrectly. In 1995, it was shown that the superflip needs 20 face turns or 24 quarter turns to solve. Later, an even harder position was found that needed 26 quarter turns!
Finding the Largest Number of Moves
At first, people who solved the cube by hand often needed around 100 moves. Early computer programs also found solutions that were quite long.
- In 1979, one method needed up to 277 moves.
- Soon after, other methods brought that number down to 160, then 94 moves.
Smart Ways to Solve the Cube
Over time, computer scientists developed clever ways to find much shorter solutions.
Thistlethwaite's Algorithm
A big step forward came from a method called "descent through nested sub-groups," created by Morwen Thistlethwaite. His idea was to break the huge problem of solving the cube into smaller, easier steps.
Instead of trying to solve everything at once, he divided the cube's state into different "groups." You would solve the cube to get it into the first group, then the second group, and so on, until it was completely solved. Each step used a specific set of moves.
This method greatly reduced the maximum number of moves needed. It went from 85, then to 80, then 63, and finally to just 45 moves at most!
Kociemba's Algorithm
In 1992, Herbert Kociemba improved Thistlethwaite's idea. He simplified it even further, using only two main groups instead of several.
This algorithm uses a computer search to find the best moves for each step. It can typically find solutions in fewer than 21 moves. In 1995, it was proven that this method could solve any cube in at most 29 face turns or 42 quarter turns. This was later improved to 40 quarter turns.
Kociemba's method uses "lookup tables" to quickly figure out the best moves. Imagine a giant cheat sheet that tells the computer exactly what to do! This makes the search super fast.
Korf's Algorithm
While the previous methods were fast, they didn't always guarantee the *absolute shortest* solution. Richard Korf, in 1997, created an algorithm that *always* finds the shortest possible solution for any given cube.
His method is called "IDA*." It works by searching for solutions of increasing length (1 move, then 2 moves, then 3, and so on). It also uses "pattern databases." These are like smaller cheat sheets for parts of the cube, such as just the corners or just certain edges. By knowing the minimum moves for these smaller parts, the algorithm can guess how many moves the whole cube might need.
Korf used this method to solve random cubes, and none of them needed more than 18 face turns.
Finding God's Number
The search for the absolute minimum number of moves, "God's Number," continued.
- In 2007, a supercomputer showed that all unsolved cubes could be solved in no more than 26 face turns.
- By 2008, this number was reduced to 23, then 22 moves.
Finally, in 2010, a team of researchers including Tomas Rokicki, Herbert Kociemba, Morley Davidson, and John Dethridge used powerful computers to prove it: any Rubik's Cube can be solved in a maximum of 20 face turns. This is God's Number for the face-turn metric!
For the quarter-turn metric, it was proven in 2014 that the maximum number of moves needed is 26.
It's interesting that for the 20-move face-turn metric, there are hundreds of millions of cube positions that actually need all 20 moves. But for the 26-move quarter-turn metric, only a very few specific positions are known to require all 26 moves.
- How to solve the Rubik's Cube, a Wikibooks article that gives an overview over several algorithms that are simple enough to be memorizable by humans. However, such algorithms will usually not give an optimal solution which only uses the minimum possible number of moves.
See also
 In Spanish: Soluciones óptimas para el cubo de Rubik para niños
In Spanish: Soluciones óptimas para el cubo de Rubik para niños