Rubik's Cube group facts for kids

The Rubik's Cube group is a special mathematical group that helps us understand how the Rubik's Cube works. Think of it as a collection of all the possible moves you can make on a Rubik's Cube. Each "element" in this group is like a specific way to twist and turn the cube's faces.
When you solve a Rubik's Cube, you're essentially finding a path through this group back to the starting "solved" position. Every single possible mixed-up state of the cube is also part of this group. The way we combine moves, like doing one twist after another, is what the group's "operation" is all about. It's like adding numbers, but with cube moves instead!
This group is built by thinking about each of the 48 colored squares (called facets) that aren't in the center. When you twist a face, these facets move around. So, every move is like a "rearrangement" of these facets. The solved cube is like the "do nothing" rearrangement. The Rubik's Cube group is created by all the basic 90-degree turns you can make on the cube.
One cool thing about this group is that it's "non-abelian." This means the order in which you do your moves matters. If you do a "Front" turn then a "Right" turn, it's usually not the same as doing a "Right" turn then a "Front" turn!
Understanding Cube Moves
A standard Rubik's Cube is a 3x3x3 puzzle. It has 6 faces, and each face has 9 colored squares called facets. When the cube is solved, all the facets on each face are the same color.
A "cube move" means turning one of the 6 faces. You can turn it 90 degrees clockwise, 180 degrees (a half-turn), or 90 degrees counter-clockwise. The center facet on each face just spins in place; it doesn't move to a different spot.
People use a special code called Singmaster notation to describe cube moves. Here's what some of the basic moves mean:
| Basic 90° | 180° | -90° |
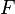 turns the front clockwise turns the front clockwise |
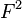 turns the front clockwise twice turns the front clockwise twice |
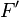 turns the front counter-clockwise turns the front counter-clockwise |
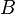 turns the back clockwise turns the back clockwise |
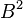 turns the back clockwise twice turns the back clockwise twice |
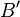 turns the back counter-clockwise turns the back counter-clockwise |
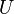 turns the top clockwise turns the top clockwise |
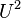 turns the top clockwise twice turns the top clockwise twice |
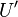 turns the top counter-clockwise turns the top counter-clockwise |
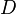 turns the bottom clockwise turns the bottom clockwise |
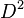 turns the bottom clockwise twice turns the bottom clockwise twice |
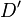 turns the bottom counter-clockwise turns the bottom counter-clockwise |
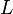 turns the left face clockwise turns the left face clockwise |
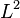 turns the left face clockwise twice turns the left face clockwise twice |
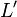 turns the left face counter-clockwise turns the left face counter-clockwise |
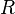 turns the right face clockwise turns the right face clockwise |
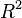 turns the right face clockwise twice turns the right face clockwise twice |
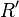 turns the right face counter-clockwise turns the right face counter-clockwise |
The "empty move" is like doing nothing at all. If you do the same move four times, it's usually like doing nothing. For example, turning the left face four times (`LLLL`) brings it back to where it started.
How Many Ways to Mix a Cube?
The Rubik's Cube group helps us count all the different ways a Rubik's Cube can be mixed up. It's a huge number!
There are exactly 43,252,003,274,489,856,000 (that's over 43 quintillion!) possible positions for a standard 3x3x3 Rubik's Cube. Even though this number is incredibly large, scientists have figured out something amazing called "God's Number."
"God's Number" for the Rubik's Cube is 20. This means that no matter how scrambled a Rubik's Cube is, you can always solve it in 20 moves or fewer. This counts a half-turn (like 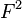 ) as one move. If you count each quarter-turn as a separate move, then God's Number is 26.
) as one move. If you count each quarter-turn as a separate move, then God's Number is 26.
Some moves, when repeated, will eventually bring the cube back to its original state. The longest sequence of moves you can make before the cube returns to its starting position is 1260 moves.
Smaller Groups Inside
Just like you can have teams within a big sports league, the Rubik's Cube group has smaller groups inside it. These are called "subgroups."
One type of subgroup focuses on "cube orientations." These are moves that keep the pieces in the same spot but might twist or flip them. Another type focuses on "cube permutations," which means moving the pieces to different spots but keeping their orientation the same.
These smaller groups help mathematicians understand the complex structure of the Rubik's Cube group. It's like breaking down a big, complicated machine into smaller, easier-to-understand parts.

