Transposition facts for kids

Transposition means to change places or move something from one spot to another. It's a word used in many different areas, like music, chess, and even biology. Think of it as shifting something from one position to another, but the exact meaning changes depending on the subject.

Transposition in Music

In music, transposition means changing the key of a song or piece of music. When you transpose music, you move all the notes up or down by a specific amount. This changes the overall pitch of the song.

Why Transpose Music?

Musicians transpose music for several reasons:

• To make a song easier for a singer to perform. A song might be too high or too low for their voice.
• To make a song easier for an instrument to play. Some instruments are better suited for certain keys.
• To change the mood or feeling of a piece. A higher key might sound brighter, while a lower key might sound darker.

How it Works

Imagine a song written in the key of C major. If you transpose it up a fifth, it would then be in the key of G major. Every single note in the song would move up by five steps on the musical scale. For example, a C note would become a G note, a D note would become an A note, and so on.

Transposition in Chess

In the game of chess, a transposition happens when the same board position is reached through a different order of moves. Chess players often study specific sequences of moves called "openings."

Understanding Transpositions in Chess

Sometimes, two different opening sequences can lead to the exact same arrangement of pieces on the board. When this happens, it's called a transposition.

• It can surprise an opponent who might be expecting a different game plan.
• It allows players to guide the game into positions they know well, even if their opponent tries a different opening.

For example, a game might start with moves that look like one common opening, but after a few more moves, it could transpose into a position typically seen in a completely different opening.

Transposition in Genetics

In genetics, transposition refers to the process where a special piece of DNA moves from one location in a genome to another. These moving DNA segments are called transposable elements or transposons. They are sometimes called "jumping genes."

What are Transposons?

Transposons are sequences of DNA that can change their position within the genome of a cell. They can move around and insert themselves into new places.

• Some transposons copy themselves before moving, so a new copy appears at a different spot while the original stays put.
• Others simply cut themselves out and re-insert elsewhere, like a "cut and paste" action.

Why are Transposons Important?

Transposons can have a big impact on an organism.

• They can cause mutations if they insert themselves into the middle of a gene, potentially disrupting its function.
• They can also carry genes with them, spreading them to new locations.
• Over long periods, transposons have played a role in the evolution of many species by rearranging genetic material.

Transposition in Mathematics

In mathematics, the transpose of a matrix is a new matrix created by flipping the original matrix over its main diagonal. This means that the rows of the original matrix become the columns of the new matrix, and the columns become the rows.

What is a Matrix?

A matrix is a rectangular arrangement of numbers, symbols, or expressions, organized into rows and columns. They are used in many areas of mathematics, science, and engineering to organize and work with data.

How to Transpose a Matrix

Let's say you have a matrix with 2 rows and 3 columns. Original Matrix: 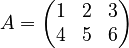Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): A = \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{pmatrix} To find its transpose, you simply swap the rows and columns. The first row (1, 2, 3) becomes the first column, and the second row (4, 5, 6) becomes the second column. Transposed Matrix (A^T): 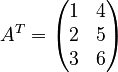Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): A^T = \begin{pmatrix} 1 & 4 \\ 2 & 5 \\ 3 & 6 \end{pmatrix} The transposed matrix now has 3 rows and 2 columns.