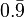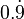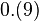0.999... facts for kids

This picture helps show how 0.999... is the same as 1.

0.999... (also written as 0.9 or 0. · ) is a special way to write the number 1. Even though it looks like it's a little bit less than 1, it's actually exactly the same! No matter how many nines you write after the decimal point, it still equals 1.

What is 0.999...?

0.999... is called a repeating decimal. This means the number "9" goes on forever after the decimal point. It's different from a number like 0.999, which only has three nines and is a tiny bit less than 1.

Sometimes, you might see 0.999... written in other ways, like:

It can be tricky for many people to understand why 0.999... is exactly the same as 1. But don't worry, there are some cool math tricks that show why they are equal!

Why 0.999... Equals 1

Mathematicians have found many ways to prove that 0.999... is the same as 1. Here are a few simple ways to think about it.

The Division Trick

Imagine you want to divide the number 1 by 3.

• If you do 1 divided by 3, you get the fraction ¹⁄₃.
• If you try to write ¹⁄₃ as a decimal, you get 0.333... (the 3s go on forever).

So, we know that ¹⁄₃ = 0.333...

Now, let's think about what happens if you multiply ¹⁄₃ by 3:

• ¹⁄₃ multiplied by 3 is ³⁄₃, which equals 1.
• If you multiply 0.333... by 3, you get 0.999... (the 9s go on forever).

Since both ¹⁄₃ multiplied by 3 and 0.333... multiplied by 3 give you the same result (just written differently), it means that 1 and 0.999... must be the same number!

The "No Space Between" Idea

Think about any two different numbers, like 1 and 2. You can always find another number in between them, like 1.5. Or between 0.9 and 1, you can find 0.95.

But what about 0.999... and 1? If you try to find a number that is bigger than 0.999... but smaller than 1, you can't! Because 0.999... has nines that go on forever, there's no "last" nine to put another digit after. This means there's no space between 0.999... and 1. If there's no number between them, they must be the same number.

The Algebra Way

Here's another way using a bit of algebra:

• Let's say `x` is equal to 0.999...
• So, `x = 0.999...`

Now, let's multiply both sides of that equation by 10:

• `10x = 9.999...`

Next, we can subtract the first equation (`x = 0.999...`) from the second one (`10x = 9.999...`):

• `10x - x = 9.999... - 0.999...`
• This simplifies to `9x = 9`

Finally, to find out what `x` is, we divide both sides by 9:

• `x = 9 / 9`
• `x = 1`

Since we started by saying `x = 0.999...` and we found that `x = 1`, it proves that `0.999... = 1`!

0.999... in Popular Discussions

This idea that 0.999... equals 1 is often a topic of discussion online. On websites where people talk about math, or even just general discussion forums, arguments about 0.999... are quite common. It's a fun way to explore how numbers work and how our brains sometimes struggle with the idea of "infinity."

See also

• In Spanish: 0,999… para niños