Algebraic fraction facts for kids
An algebraic fraction is like a regular fraction, but instead of just numbers, it has algebraic expressions on the top and bottom. Think of it as a way to show division using algebra. For example, 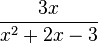 is an algebraic fraction.
is an algebraic fraction.
A rational fraction is a special type of algebraic fraction. It has polynomials on both the top and bottom. A polynomial is an expression where variables (like `x`) only have whole number powers (like `x^2` or `x^3`), and there are no square roots of variables. The fraction 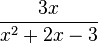 is a rational fraction because both the top (`3x`) and the bottom (`x^2+2x-3`) are polynomials. However,
is a rational fraction because both the top (`3x`) and the bottom (`x^2+2x-3`) are polynomials. However, 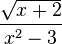 is not a rational fraction because the top has a square root of a variable.
is not a rational fraction because the top has a square root of a variable.
Contents
How to Work with Algebraic Fractions
Working with algebraic fractions is similar to working with regular fractions. You can multiply them, divide them, add them, and subtract them.
Multiplying Algebraic Fractions
To multiply algebraic fractions, you multiply the tops (numerators) together and the bottoms (denominators) together. Often, you can simplify the fractions before or after multiplying by canceling out common parts.
Let's look at an example: 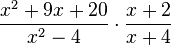
First, you can factor the expressions on the top and bottom:
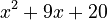 factors to
factors to 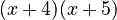
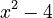 factors to
factors to 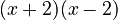 (this is a difference of squares)
(this is a difference of squares)
So the problem becomes: 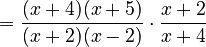
Now, you can see that 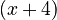 is on the top and bottom, and
is on the top and bottom, and 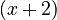 is also on the top and bottom. You can cancel these out:
is also on the top and bottom. You can cancel these out: 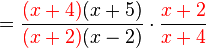
After canceling, you are left with: 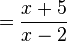
This is the simplified answer.
Dividing Algebraic Fractions
To divide algebraic fractions, you change the division problem into a multiplication problem. You do this by "flipping" the second fraction (finding its reciprocal) and then multiplying.
Here's how it works: 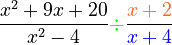
Flip the second fraction (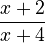 becomes
becomes 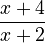 ) and change the division sign to multiplication:
) and change the division sign to multiplication: 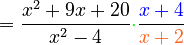
Now, this is a multiplication problem, just like the one we solved above. You would factor the expressions and cancel out common terms to simplify the answer.
See also
 In Spanish: Fracción algebraica para niños
In Spanish: Fracción algebraica para niños

