Balance puzzle facts for kids

An animation of a solution to the a false coin problem involving ten coins. In this example, the false coin is lighter than the others.

A balance puzzle is like a fun detective game! You use a balance scale to figure out which item, usually a coin, is different from the others. Maybe it's lighter or heavier. The cool part is, you don't need to know the exact weight. You just need to compare items to each other. These puzzles challenge your logic and problem-solving skills!

Imagine you have a bunch of coins, and one of them is fake. It might be a little lighter or a little heavier than the real ones. Your job is to find that fake coin using a balance scale only a few times.

For example, with three weighings, you can usually figure out which coin is different from a group of up to 13 coins. If you have 12 coins, you can even find out if the different coin is heavier or lighter.

Nine-Coin Problem: Finding a Lighter Coin

Solution to the balance puzzle for 9 coins in 2 weighings, where the odd coin is lighter than the others.

Here's a classic puzzle: You have nine coins. Eight of them are exactly the same weight, but one is a fake and is lighter than the others. Can you find the lighter coin using a balance scale only two times?

How to Solve It

First, let's think about how many coins you can check in just one weighing. You can check up to three coins. Here's how:

• Put one coin on the left side of the scale and another on the right.
• If they balance, the lighter coin must be the one you left off the scale.
• If one side goes up, that coin is the lighter one.

Now, let's go back to the nine coins.

• Weighing 1: Divide the nine coins into three groups of three coins each.
  • Take two of these groups (three coins from group A and three coins from group B). Put group A on the left side of the scale and group B on the right.
  • If the scale balances, it means the lighter coin is in the third group (group C), which you didn't weigh.
  • If one side goes up, that group contains the lighter coin. For example, if group A goes up, the lighter coin is in group A.
• Weighing 2: Now you know which group of three coins has the lighter one.
  • Take the three coins from that lighter group.
  • Put one coin on the left side of the scale and another on the right.
  • If they balance, the lighter coin is the third coin you didn't weigh.
  • If one side goes up, that coin is the lighter one.

So, in just two weighings, you can find the single lighter coin out of nine! If you had 27 coins, it would only take three weighings. For 81 coins, it would take four weighings.

Twelve-Coin Problem: Finding a Different Coin (Heavier or Lighter)

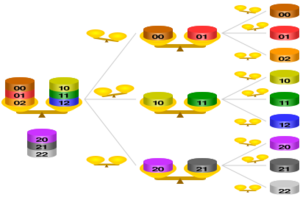
This puzzle is a bit trickier! You have twelve coins. Eleven of them are identical, but one is different. You don't know if this different coin is heavier or lighter than the others. Can you find the unique coin and figure out if it's heavier or lighter, using the balance scale only three times?

This puzzle was first shared in 1945. There are many ways to solve it!

One Way to Solve It

• Weighing 1: Put four coins on the left side of the scale and four coins on the right side. Keep the remaining four coins off to the side.
  • Possibility 1: The scale tips (one side is heavier).
    • This means the different coin is among the eight coins you just weighed. It's either a heavy coin on the heavier side or a light coin on the lighter side. The four coins you left out are all normal.
  • Possibility 2: The scale balances.
    • This means all eight coins you just weighed are normal. The different coin must be one of the four coins you left off the scale.

Let's look at what happens next for each possibility:

If the Scale Tipped in Weighing 1

(Let's say coins 1,2,3,4 were on the left and 5,6,7,8 on the right. If the left side was heavier, then either 1,2,3, or 4 is heavy, OR 5,6,7, or 8 is light.)

• Weighing 2:
  • Take three coins from the original heavier side (e.g., 1,2,3) and remove them.
  • Take three coins from the original lighter side (e.g., 5,6,7) and move them to the heavier side of the scale (where 1,2,3 were).
  • Take three normal coins (from the group that balanced in Weighing 1, or from the unweighed group if Weighing 1 tipped) and put them on the lighter side of the scale (where 5,6,7 were).
  • The remaining coins (4 from the original heavier side, 8 from the original lighter side, and the 4 unweighed coins) are set aside.

Now, there are three outcomes for Weighing 2:

• Outcome A: The same side is still heavier.
  • This means the heavy coin is the one that stayed on the heavier side (coin 4). Or, the light coin is the one that stayed on the lighter side (coin 8).
  • Weighing 3: Compare coin 4 with a normal coin. If 4 is heavier, it's the fake. If it balances, then coin 8 is the light fake.
• Outcome B: The side that was heavier in Weighing 1 is now lighter.
  • This means one of the three coins that moved from the lighter side to the heavier side (coins 5,6,7) is the light coin.
  • Weighing 3: Weigh two of these three coins (e.g., 5 and 6) against each other. If one is lighter, that's the fake. If they balance, then coin 7 is the light fake.
• Outcome C: Both sides are now even.
  • This means one of the three coins you removed from the original heavier side (coins 1,2,3) is the heavy coin.
  • Weighing 3: Weigh two of these three coins (e.g., 1 and 2) against each other. If one is heavier, that's the fake. If they balance, then coin 3 is the heavy fake.

If the Scale Balanced in Weighing 1

(This means the first eight coins are all normal. The different coin is one of the four coins you didn't weigh.)

• Weighing 2: Take three of these four remaining coins (let's call them A, B, C). Put them on one side of the balance. Put three of the eight normal coins (from Weighing 1) on the other side. The fourth unweighed coin (D) is set aside.
• Outcome A: The three coins (A,B,C) are lighter.
  • This means one of A, B, or C is the fake coin, and it's lighter.
  • Weighing 3: Weigh two of these three coins (e.g., A and B) against each other. If one is lighter, that's the fake. If they balance, then C is the light fake.
• Outcome B: The three coins (A,B,C) are heavier.
  • This means one of A, B, or C is the fake coin, and it's heavier.
  • Weighing 3: Weigh two of these three coins (e.g., A and B) against each other. If one is heavier, that's the fake. If they balance, then C is the heavy fake.
• Outcome C: The three coins (A,B,C) balance.
  • This means A, B, and C are all normal. So, the fourth coin (D) is the fake one.
  • Weighing 3: Weigh coin D against any of the normal coins. If D is lighter, it's a light fake. If D is heavier, it's a heavy fake. If it balances, then all coins are normal (which is also a possible outcome for the 12-coin problem).

Variations

Imagine you have 13 coins, and you know for sure that one of them is different (either heavier or lighter). You can find it in 3 weighings:

• Step 1: Divide the coins into two groups of 4 coins each, and a third group with the remaining 5 coins.
• Weighing 1: Weigh the two groups of 4 coins against each other.
  • If they balance: The different coin is in the group of 5 coins.
  • If they don't balance: The different coin is among the 8 coins you just weighed. You can then use a similar method to the 12-coin problem to find it.
• If the different coin is in the group of 5:
  • Weighing 2: Take 3 coins from the group of 5 and weigh them against any 3 normal coins (from the group of 8 that balanced in Weighing 1).
    • If they balance: The different coin is among the remaining 2 coins from the original group of 5.
      • Weighing 3: Weigh one of these 2 coins against any other normal coin. If they balance, the other coin is the fake. If they don't balance, the one you weighed is the fake.
    • If they don't balance: The different coin is from the group of 3 coins you just weighed. Pay attention to which side went up or down (lighter or heavier).
      • Weighing 3: Remove one of the 3 coins. Move another to the other side of the balance. If the balance evens out, the coin you removed is the fake. If the balance switches direction, the coin you moved is the fake. Otherwise, the coin that stayed in place is the fake.

See also

In Spanish: Problema de las doce monedas para niños