Bell's theorem facts for kids

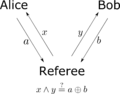
Bell's theorem, also known as "Bell's inequality," is a cool idea that helps us understand how tiny particles work. It's like a thought experiment combined with real tests. This theorem shows that some strange things in quantum mechanics can't be explained by secret, hidden rules. A smart scientist named John Stewart Bell came up with this idea.

Brian Greene's analogy

Understanding Bell's Theorem

To get a better idea of Bell's theorem, let's look at an example from scientist Brian Greene. Imagine you have pairs of special boxes. One box goes to Earth, and the other goes to a faraway planet called Vulcan.

The Mystery Boxes

Each box has three doors: a gray door, a white door, and a black door. Inside, there's a light that turns on when you open a door. The light will be either blue or red.

If people on Earth and Vulcan open the same door on their boxes (like both open the gray door), the lights will always match. Both will be blue, or both will be red.

But what happens if they open different doors? For example, Earth opens the gray door, and Vulcan opens the black door.

Hidden Rules or Quantum Magic?

There are two main ideas about how these lights work:

• Idea 1: Hidden Rules (or "Hidden Variables") Maybe the color of the light for each door was already decided when the boxes were made. It's like a secret code inside each box. If this is true, then when you open different doors, you'd expect the lights to match more often than not. Scientists calculated this to be about 55% of the time or more.
• Idea 2: Quantum Mechanics This idea says that the color isn't decided until the door is actually opened. It's like a coin flip happens at the very moment you open the door. Quantum physics predicts that if you open different doors, the lights should only match about 50% of the time.

What Experiments Show

Scientists have done real experiments that are like opening these mystery boxes. They found that when "different doors" are opened, the lights (or particle properties) only match about 50% of the time. This is exactly what quantum mechanics predicts!

This means there are no "hidden rules" or secret codes inside the particles that decide their properties beforehand. The particles truly behave in a way that is decided at the moment they are measured. This is a very strange and important discovery about our universe!

Images for kids

• 

  An illustration of the CHSH game: the referee, Victor, sends a bit each to Alice and to Bob, and Alice and Bob each send a bit back to the referee.

• 

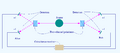
  Scheme of a "two-channel" Bell test The source S produces pairs of "photons", sent in opposite directions. Each photon encounters a two-channel polariser whose orientation (a or b) can be set by the experimenter. Emerging signals from each channel are detected and coincidences of four types (++, −−, +− and −+) counted by the coincidence monitor.

See also

In Spanish: Teorema de Bell para niños