Board puzzles with algebra of binary variables facts for kids

Board puzzles with algebra of binary variables are like treasure hunts on a grid! Your goal is to find hidden objects based on clues. These clues are numbers in certain cells. Each cell on the board can either have an object (which we call a 1) or be empty (which we call a 0).

What are These Puzzles About?

These puzzles use a special kind of math called binary algebra. "Binary" just means there are only two choices, like "yes" or "no," "true" or "false," or in our case, 0 (empty) or 1 (has an object).

You'll need to figure out simple math problems, like equations, to solve the puzzle. Sometimes, you can even break the puzzle into smaller parts to make it easier. If a puzzle is designed to have only one correct answer, that can also help you figure things out without doing lots of calculations.

Understanding Binary Algebra

In these puzzles, we use letters like a, b, or c to stand for cells on the board. Each letter can only be a 0 (empty) or a 1 (has an object).

Let's look at some simple examples:

• a + b = 0

* Here, a and b can only be 0 or 1. The only way their sum can be 0 is if both a is 0 and b is 0.

• a + b = 2

* For this to be true, both a and b must be 1. (Because 1 + 1 = 2).

Here's a slightly trickier one:

• a + b + c = 2
• a + b ≤ 1 (This means a + b can be 0 or 1)

From the second line, we know a and b can't both be 1. So, here are the possibilities for a and b:

1. a = 1 and b = 0
2. a = 0 and b = 1
3. a = 0 and b = 0

If a and b were both 0 (case 3), then the first equation would be 0 + 0 + c = 2, which means c would have to be 2. But c can only be 0 or 1. So, case 3 is impossible! This means either case 1 or case 2 must be true. In both cases, a + b equals 1. If a + b = 1, then from the first equation (a + b + c = 2), we get 1 + c = 2. This means c must be 1.

You can also simplify bigger equations. For example:

• a + b + c + d = 3
• c + d = 1

Since we know c + d equals 1, we can replace that part in the first equation: a + b + 1 = 3 This simplifies to:

• a + b = 2
• c + d = 1

Playing Algebra on a Board

Figure 1: An example puzzle on a 4x4 board

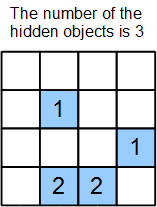
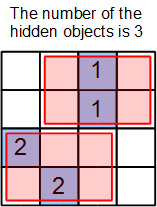
These puzzles are often played on a grid, like the one in Figure 1. Some cells are "clue cells" (blue background), and they have a number. This number tells you how many hidden objects are in the cells right next to it. These "neighbor" cells are the ones that can have a 0 or a 1. Neighbors include cells touching a side or a corner.

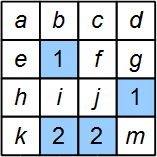
The white cells are the ones that might have hidden objects. They are our binary variables. The total number of objects on the whole board might also be given as a clue. Figure 2 shows the same board with the variables (letters) marked.

Turning the Puzzle into Equations

Figure 2: Binary variables are marked

First, if given, write an equation for the total number of hidden objects on the board. For Figure 1 and 2, let's say the total is 3:

a + b + c + d + e + f + g + h + i + j + k + m = 3

Next, create an equation for each clue cell. The number in the clue cell tells you the sum of its neighbors.

• The clue cell in the top left (with the number 1) has these neighbors:

 :a + b + c + e + f + h + i + j = 1

• The clue cell in the top right (with the number 1) has these neighbors:

 :f + g + j + m = 1

• The clue cell in the bottom left (with the number 2) has these neighbors:

 :h + i + j + k = 2

• The clue cell in the bottom right (with the number 2) has these neighbors:

 :i + j + m = 2

Now, let's solve this example step-by-step:

1. We know i + j + m = 2 (from the bottom right clue). Look at the clue cell in the top right (with the number 1). Its neighbors are f, g, j, and m. This means j and m are neighbors of a cell that can only have one object. So, j + m can be at most 1.

Since i + (j + m) = 2, and j + m is at most 1, then i must be 1. (If j + m was 0, i would be 2, which is impossible. If j + m was 1, i would be 1). So, i = 1.

1. Since i = 1, and i is a neighbor of the top-left clue cell (which sums to 1), all the other neighbors of that clue cell must be 0.

So, a, b, c, e, f, h, and j must all be 0.

1. 

   Figure 3: The example solved partially

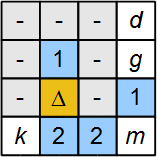
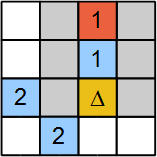
Now look at Figure 3. The gray cells with '–' are 0. The cell with 'Δ' is 1 (which is i from step 1). Consider the bottom-left clue cell (with the number 2). Its neighbors are h, i, j, and k. We know h = 0, i = 1, and j = 0. So, 0 + 1 + 0 + k = 2. This means 1 + k = 2, so k must be 1.

1. Similarly, for the bottom-right clue cell (with the number 2). Its neighbors are i, j, and m. We know i = 1 and j = 0.

So, 1 + 0 + m = 2. This means 1 + m = 2, so m must be 1.

1. 

   Figure 4: The example solved

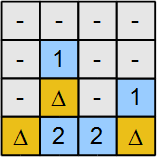
We have found three objects: i = 1, k = 1, and m = 1. Remember the very first equation: a + b + c + d + e + f + g + h + i + j + k + m = 3. Since we found three objects, all other variables must be 0. So, d = 0 and g = 0. Figure 4 shows the final solution!

Using the Idea of a Unique Solution

Sometimes, a puzzle is designed to have only one correct answer. This is called a "unique solution." For example, in Figure 2, the variables a, b, c, and e are only neighbors to the top-left clue cell (which has a 1). If any one of these (a, b, c, or e) was 1, and the others were 0, it would satisfy that clue. But if the puzzle says there's only ONE way to solve it, then these variables (a, b, c, e) must all be 0. Why? Because if any of them were 1, there would be multiple possible solutions for that part of the puzzle, which goes against the "unique solution" rule.

Breaking the Puzzle into Parts (Partitioning)

Figure 5: An example for partitioning

Some puzzles can be split into smaller, separate sections. This is called "partitioning." Each section might have a certain number of hidden objects. The total number of objects in all sections should add up to the total for the whole board.

In Figure 5, the red transparent zones show how the puzzle can be partitioned. The cells outside these zones (the all-white cells) must be empty. This means they contain no hidden objects. By breaking it down, you can solve each smaller part more easily.

Trying and Checking (Try-and-Check Method)

Figure 6: An example for try-and-check method

Sometimes, you can try placing an object (setting a variable to 1) in a cell and see what happens. If your guess leads to a problem or a contradiction, then you know that cell must be empty (it's a 0).

Look at Figure 6. Let's say we try to put an object in the cell marked with 'Δ' (let's call this variable f = 1). If f is 1, then all its neighbors that belong to the clue cell with the number 1 (marked in red) must be 0. So, a, b, c, d, e, and g would all be 0. But if a, b, c, and d are all 0, then their sum (which is the clue cell's value) would be 0. However, the clue cell is a 1. This is a contradiction! Since our guess (f = 1) led to a contradiction, we know that f must actually be 0.

This "try-and-check" method can be very useful for solving tricky parts of a puzzle.

How Hard Can These Puzzles Get?

The difficulty of these puzzles can be changed in a few ways. One way is to change how many clue cells there are compared to the total number of cells. However, this doesn't always make the difficulty consistent.

Another way to make them harder is to require more complex thinking steps, like needing to subtract equations or using the try-and-check method multiple times. As the board gets bigger, the puzzles usually become more complex too. The number of hidden objects on the board also affects how hard the puzzle is.