Cauchy–Kowalevski theorem facts for kids

The Cauchy–Kovalevskaya theorem is a very important idea in mathematics. It helps us understand if special kinds of math problems, called partial differential equations, have solutions and if those solutions are unique (meaning there's only one answer). This theorem is especially for problems where the functions involved are "analytic." An analytic function is one that can be written as an endless sum of simpler terms, like a Taylor series.

A special part of this theorem was first shown by a mathematician named Augustin Cauchy in 1842. Later, the full and more general version was proven by a brilliant mathematician named Sofia Kovalevskaya in 1875.

What is the First Order Cauchy–Kovalevskaya Theorem?

This theorem talks about finding solutions to a group of equations called "differential equations." These equations involve how things change. Imagine you have a function that describes something, and you want to know how it changes over time or space. Differential equations help with that.

The theorem says that if you have a system of these equations where the parts of the equations (called coefficients) are "analytic functions" (meaning they are very smooth and predictable), then there's a special kind of solution that exists and is unique. This solution is also an analytic function.

Think of it like this: If you have a very well-behaved puzzle (where all the pieces are perfectly shaped and fit together smoothly), this theorem tells you that there's a unique way to solve that puzzle in a small area.

The theorem works for functions that use either real numbers or complex numbers.

Sometimes, even if functions seem smooth, they might not be "analytic." For example, a famous case called Lewy's example showed that if the functions aren't analytic, the theorem might not work, and there might be no solution at all!

How the Proof Works (A Simple Idea)

The way mathematicians prove this theorem is quite clever. They imagine the solutions as formal power series. A power series is like an endless polynomial, for example, `a + bx + cx^2 + dx^3 + ...`.

They can figure out what each part (coefficient) of this endless series should be. It turns out that these coefficients are determined in a unique way.

Then, they compare the original complex problem to a simpler, related problem. This simpler problem has an answer that they know converges (meaning the endless sum doesn't go to infinity, but settles on a specific number). They show that the solutions to the original problem are "majorized" by the solutions to the simpler problem. This means the numbers in the original problem's solution are always smaller than or equal to the numbers in the simpler problem's solution.

Because the simpler problem's solution converges, it helps them prove that the original problem's solution must also converge, meaning it's a real, existing analytic solution.

Higher-Order Cauchy–Kovalevskaya Theorem

The theorem also applies to more complex differential equations, called "higher-order" equations. This means the equations involve more steps of change (like how speed changes, and how that change itself changes).

If you have a non-linear (more complicated) differential equation and its starting conditions are analytic functions, then there's a unique analytic solution near the starting point.

An Example: The Heat Equation

Let's look at the heat equation. This equation describes how heat spreads through something over time. It looks like this:

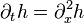
This means "how heat changes over time" equals "how heat changes in space, twice."

If you set a starting condition, like how hot something is at a specific time (say, `t = 0`), the theorem says there should be a unique analytic solution.

However, there's a catch! For the heat equation, if you pick a specific starting condition like `h(0,x) = 1 / (1 + x^2)`, the formal power series solution (the endless sum we talked about) doesn't always converge for any time `t` that isn't zero. This means that even though you can write down a theoretical solution, it doesn't actually work in the real world as an analytic function for all times.

This example, first shown by Kovalevskaya herself, teaches us that the conditions for the theorem are very important. The theorem doesn't work for all types of differential equations, especially if they don't meet the strict "analytic" requirements in a certain way.

See also

In Spanish: Teorema de Cauchy-Kovalévskaya para niños