Conditional probability Facts for Kids

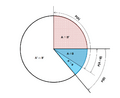
Imagine you want to know the chance of something happening, but you already have some important information. That's where conditional probability comes in! It's about figuring out the chance of an event happening, knowing that another event has already happened. We write it like 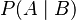$P(A\mid B)$ . This means "the probability of event A happening, given that event B has already happened." The two events don't have to be connected, and they don't need to happen at the same time.

What is Conditional Probability?
- How Do We Calculate It?
- Real-Life Examples
  - Example: Rolling a Die
  - Example: Drawing Cards
Images for kids
See also

What is Conditional Probability?

Conditional probability is a super useful idea in probability theory. It helps us understand how likely an event is to happen when we already know something else has occurred. Think of it like this: if you know it's cloudy outside, the chance of rain might be higher than if you didn't know anything about the clouds. The "cloudy outside" part is the condition!

How Do We Calculate It?

To find the conditional probability of event A happening, given that event B has already happened, we use a special formula: 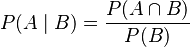$P(A\mid B) = \frac{P(A\cap B)}{P(B)}$

Let's break down what this means:

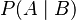$P(A\mid B)$ is the probability of A happening, given B.
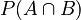Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): P(A\cap B) is the probability that both event A and event B happen together. This is sometimes called the "intersection" of A and B.
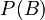Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): P(B) is the probability that event B happens.

It's important that the probability of event B (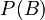Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): P(B) ) is not zero. If 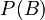Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): P(B) were zero, it would mean event B can't happen, and then we couldn't use it as a condition.

Real-Life Examples

Let's look at some examples to make this clearer.

Example: Rolling a Die

Imagine you roll a standard six-sided die.

Let event A be "rolling a 6".
Let event B be "rolling an even number" (2, 4, or 6).

What is the probability of rolling a 6, given that you rolled an even number?

The possible outcomes when rolling a die are {1, 2, 3, 4, 5, 6}.
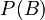Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): P(B) (probability of rolling an even number) = 3 out of 6 outcomes = 3/6 = 1/2.
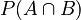Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): P(A\cap B) (probability of rolling a 6 AND an even number) = Only one outcome (6) fits this. So, 1 out of 6 outcomes = 1/6.

Now, let's use the formula: 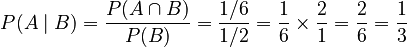Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): P(A\mid B) = \frac{P(A\cap B)}{P(B)} = \frac{1/6}{1/2} = \frac{1}{6} \times \frac{2}{1} = \frac{2}{6} = \frac{1}{3} So, the probability of rolling a 6, given that you rolled an even number, is 1/3. This makes sense because if you know it's an even number, your choices are 2, 4, or 6, and 6 is one of those three.

Example: Drawing Cards

Let's say you draw one card from a standard deck of 52 playing cards.

Let event A be "drawing a King".
Let event B be "drawing a face card" (King, Queen, or Jack).

What is the probability of drawing a King, given that you drew a face card?

There are 4 Kings in a deck.
There are 12 face cards (4 Kings, 4 Queens, 4 Jacks).
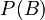Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): P(B) (probability of drawing a face card) = 12 out of 52 cards = 12/52.
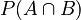Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): P(A\cap B) (probability of drawing a King AND a face card) = All Kings are face cards, so this is just the probability of drawing a King = 4 out of 52 cards = 4/52.

Using the formula: 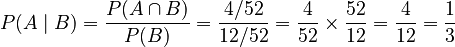Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): P(A\mid B) = \frac{P(A\cap B)}{P(B)} = \frac{4/52}{12/52} = \frac{4}{52} \times \frac{52}{12} = \frac{4}{12} = \frac{1}{3} So, the probability of drawing a King, given that you drew a face card, is 1/3. If you know you have a face card, it must be a King, Queen, or Jack, and a King is one of those three.

Images for kids

Venn Pie Chart describing conditional probabilities

Conditional probability facts for kids

Contents