Decagon facts for kids
A decagon is a flat shape, also called a polygon, that has 10 straight sides and 10 corners. Think of it like a stop sign, but with 10 sides instead of 8!
Contents
What is a Regular Decagon?
A regular decagon is a special kind of decagon where all its 10 sides are exactly the same length. Also, all its 10 corners (or angles) are the same size. Each corner in a regular decagon measures 144 degrees. If you add up all the angles inside a regular decagon, they total 1440 degrees.
Finding the Area
The area of a shape is the amount of space it covers. For a regular decagon, there's a math formula to figure out its area if you know the length of one of its sides.
How Decagons Can Be Divided
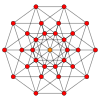
Imagine you have a regular decagon. You can actually cut it into smaller shapes! A mathematician named Harold Scott MacDonald Coxeter found that a regular decagon can be divided into 10 smaller shapes called rhombs. A rhomb is like a squished square, where all four sides are equal in length.
You can see different ways a regular decagon can be cut into these 10 rhombs:
 |
 |
 |
 |
 |
 |
 |
 |
What is a Skew Decagon?
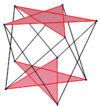
A skew decagon is a shape that also has 10 corners and 10 edges, but it's not flat. Instead, its corners and edges zig-zag in 3D space, meaning they don't all lie on the same flat surface.
A special type is a skew zig-zag decagon, where its corners go back and forth between two flat surfaces that are parallel to each other.
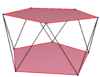
You can see examples of regular skew decagons as the zig-zagging edges of certain 3D shapes, like the ones shown below:
| {5}#{ } | {5/2}#{ } | {5/3}#{ } |
|---|---|---|
 |
 |
 |
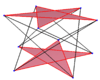| These images show regular skew decagons as zig-zagging edges of different 3D shapes. | ||
These zig-zagging decagons can also be found when looking at certain 3D shapes from specific angles. The outlines of these shapes, when projected flat, can form regular skew decagons.
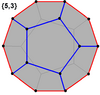 Dodecahedron |
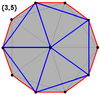 Icosahedron |
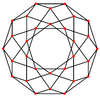 Icosidodecahedron |
 Rhombic triacontahedron |
Related Shapes and Ideas
- Decagonal number and centered decagonal number: These are special numbers that can be shown as dots arranged in the shape of a decagon.
- Decagram: This is a star-shaped polygon that has the same corner positions as a regular decagon.
- Eric W. Weisstein, Decagon at MathWorld.
Images for kids
-
Symmetries of a regular decagon. This image shows how a decagon can be folded or turned and still look the same.
See also
In Spanish: Decágono para niños
