Diffie–Hellman key exchange facts for kids

In the Diffie–Hellman key exchange, two people, like Alice and Bob, create a secret code together. They share some public information, but their private secrets stay hidden. This lets them make a shared secret key that only they know. They can then use this key to send secret messages to each other.

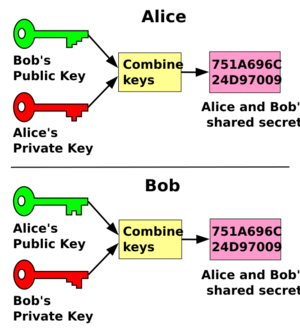
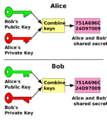
The Diffie–Hellman key exchange is a clever mathematical method that allows two people to create a shared secret code over an open, public channel. Imagine you want to send a secret message to a friend, but you've never met in person to agree on a secret code. This method helps you do just that! It was one of the very first "public-key" systems, meaning it uses two keys: a public one that everyone can see, and a private one that only you know.

This idea was first thought of by Ralph Merkle. Later, Whitfield Diffie and Martin Hellman published the method in 1976. Before this, if you wanted to send a secret message, you had to physically share the secret code first, perhaps by sending a trusted messenger with a list of codes. Diffie–Hellman changed that. It lets two people who don't know each other make a secret key together, even if someone else is listening in on their conversation. This secret key can then be used to encrypt (scramble) their messages so only they can read them.

Diffie–Hellman is used to keep many things safe on the internet. However, some older versions of this method might not be strong enough against very powerful attackers, like government spy agencies.

In 1997, it was found that British scientists James H. Ellis, Clifford Cocks, and Malcolm J. Williamson had actually discovered similar public-key ideas back in 1969. But their work was kept secret for many years.

Even though Diffie–Hellman itself doesn't check if the people talking are truly who they say they are, it's a building block for many secure internet protocols. For example, it helps keep your online connections private when you browse websites using Transport Layer Security (TLS).

Name

In 2006, Martin Hellman suggested that the method should also include Ralph Merkle's name. He felt it should be called the Diffie–Hellman–Merkle key exchange. This is because Merkle came up with the basic idea of public-key sharing.

The system...has since become known as Diffie–Hellman key exchange. While that system was first described in a paper by Diffie and me, it is a public key distribution system, a concept developed by Merkle, and hence should be called 'Diffie–Hellman–Merkle key exchange' if names are to be associated with it. I hope this small pulpit might help in that endeavor to recognize Merkle's equal contribution to the invention of public key cryptography.

How it Works

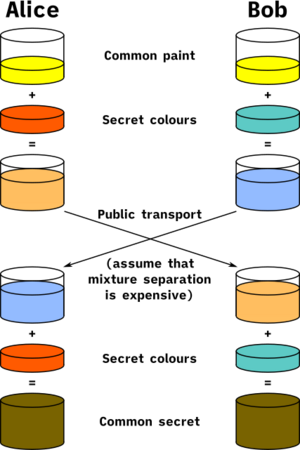
A Simple Color Analogy

This image shows the steps of the Diffie–Hellman key exchange using colors. Both Alice and Bob end up with the same secret color, which an eavesdropper cannot easily figure out.

Let's imagine how Diffie–Hellman works using colors instead of super big numbers. This helps us understand the main idea:

• Step 1: Agree on a Public Color. Alice and Bob publicly agree on a starting color. Let's say they pick yellow. Everyone, even someone listening in, knows this color.
• Step 2: Pick Secret Colors. Alice secretly chooses her own color, say red. Bob secretly chooses his own color, say cyan. They keep these colors private.
• Step 3: Mix and Share.

* Alice mixes her secret red with the public yellow. This makes a new color, say orange-tan. She sends this orange-tan mixture to Bob. * Bob mixes his secret cyan with the public yellow. This makes a new color, say light-blue. He sends this light-blue mixture to Alice. * Someone listening would only see the orange-tan and light-blue mixtures.

• Step 4: Final Mix.

* Alice takes the light-blue mixture she got from Bob and mixes it with her own secret red. This creates a final color, say yellow-brown. * Bob takes the orange-tan mixture he got from Alice and mixes it with his own secret cyan. This also creates the exact same final color, yellow-brown.

Now, Alice and Bob both have the same secret yellow-brown color. Someone listening would only know the public yellow and the two mixed colors (orange-tan and light-blue). It would be extremely difficult for them to figure out the final secret yellow-brown color. In real life, instead of colors, we use very large numbers, which makes it practically impossible for computers to guess the secret.

The Math Behind It

The real Diffie–Hellman method uses math with very large numbers. Here's a simplified look at how it works:

1. Alice and Bob agree on two public numbers: a big prime number p (like 23) and a base number g (like 5). Everyone knows these numbers.
2. Alice chooses a secret number, let's call it a (like 4). She calculates g raised to the power of a, then finds the remainder when divided by p. She sends this result, A, to Bob.

* Example: A = 5⁴ mod 23 = 4.

1. Bob chooses his own secret number, b (like 3). He calculates g raised to the power of b, then finds the remainder when divided by p. He sends this result, B, to Alice.

* Example: B = 5³ mod 23 = 10.

1. Alice takes the number B she got from Bob and raises it to her secret number a. She then finds the remainder when divided by p. This gives her the shared secret s.

* Example: s = 10⁴ mod 23 = 18.

1. Bob takes the number A he got from Alice and raises it to his secret number b. He then finds the remainder when divided by p. This also gives him the shared secret s.

* Example: s = 4³ mod 23 = 18.

Both Alice and Bob now have the same secret number (18 in this example). Only their secret numbers a and b are kept hidden. All the other numbers are sent openly. The strength of this method comes from the fact that it's incredibly hard for someone listening to figure out the secret number s just from the public numbers. This is known as the discrete logarithm problem. Even the fastest computers can't solve it in a reasonable time if the numbers are large enough (hundreds of digits long).

Who Knows What?

This chart shows what Alice, Bob, and an eavesdropper (Eve) know during the process. Secret numbers are in red and public numbers are in blue.

• g, public base: 5 (known to Alice, Bob, Eve)
• p, public prime number: 23 (known to Alice, Bob, Eve)
• a, Alice's secret: 6 (only Alice knows)
• b, Bob's secret: 15 (only Bob knows)
• A, Alice's public number: 8 (known to Alice, Bob, Eve)
• B, Bob's public number: 19 (known to Alice, Bob, Eve)

The secret number s is now known to Alice and Bob, but not to Eve.

Security

The Diffie–Hellman method is considered safe from eavesdroppers if the numbers p and g are chosen carefully. The numbers need to be very large, especially if the same numbers are used for a lot of communication. An eavesdropper would have to solve a very hard math problem (the discrete logarithm problem) to find the secret key.

If Alice and Bob use random number generators that aren't truly random, it becomes easier for someone to listen in.

One weakness of the basic Diffie–Hellman method is that it doesn't check if the people talking are who they say they are. This means it can be tricked by a "man-in-the-middle" attack.

Man-in-the-Middle Attack

Imagine a bad guy named Mallory. Mallory can pretend to be Alice when talking to Bob, and pretend to be Bob when talking to Alice.

• Mallory sets up a secret key exchange with Alice, pretending to be Bob.
• Mallory also sets up a separate secret key exchange with Bob, pretending to be Alice.

Now, when Alice sends a message to Bob, she encrypts it with the key she shares with Mallory. Mallory decrypts it, reads it, then re-encrypts it with the key she shares with Bob, and sends it to Bob. Bob thinks it came from Alice. Mallory does the same thing for messages going from Bob to Alice.

This means Mallory can read and even change all the messages between Alice and Bob without them knowing. To stop this, other methods are often used with Diffie–Hellman to make sure Alice and Bob are really talking to each other.

Real-World Attacks

Some older Diffie–Hellman setups on the internet use numbers that are not big enough (1024 bits or less). Smart attackers can use powerful computers to pre-calculate parts of the math problem for these smaller numbers. This makes it much easier for them to break the secret codes later.

Experts believe that very powerful groups, like national spy agencies, might be able to break codes that use 1024-bit numbers. To be safe, it's recommended to use much larger numbers, at least 2048 bits long, for Diffie–Hellman. This makes it incredibly harder for anyone to break the code.

Other Uses

Forward Secrecy

Some secure communication methods use Diffie–Hellman to create a brand new secret key for every single conversation or "session." This is called forward secrecy. It means that even if someone manages to steal one of your long-term secret keys later, they won't be able to decrypt your past conversations because each conversation used a different, temporary key that was thrown away.

Password-Protected Key Exchange

If Alice and Bob already share a simple password, they can use a special version of Diffie–Hellman. This helps prevent man-in-the-middle attacks. The password makes it much harder for an attacker to guess the secret key, even if they try many times.

Public Key Encryption

Diffie–Hellman can also be used as part of a system where Bob can encrypt a message so only Alice can read it, even if they've never talked before. Alice would have a public key (like her public number A and the shared g and p). Bob would use this public key to create a shared secret with Alice, then use that secret to encrypt his message. Only Alice, with her private secret number, could then decrypt it.

However, another method called RSA is more commonly used for this type of public key encryption today.

Images for kids

• 

  In the Diffie–Hellman key exchange scheme, each party generates a public/private key pair and distributes the public key. After obtaining an authentic copy of each other's public keys, Alice and Bob can compute a shared secret offline. The shared secret can be used, for instance, as the key for a symmetric cipher.

• 

  Illustration of the concept behind Diffie–Hellman key exchange