Diffie-Hellman key exchange facts for kids
The Diffie-Hellman key exchange is a clever way for two people to secretly share a special number, even if someone else is listening. It's like agreeing on a secret code without ever saying the code out loud. This method is also sometimes called an Exponential key exchange.
Contents
How This Secret Sharing Method Began
In 1976, two smart people named Whitfield Diffie and Martin Hellman came up with this idea. They wanted to find a safe way for computers to talk to each other. Their idea was inspired by Ralph Merkle's work.
Imagine you have a secret password you want to share with a friend. If you just tell them the password, someone else might hear it. Diffie-Hellman helps you share a secret number without anyone else knowing what it is. It's a way for two people to agree on a secret key. They don't even need to prove who they are to each other first. But both people need their own secret part to make the system work.
How Diffie-Hellman Works (A Simple Example)
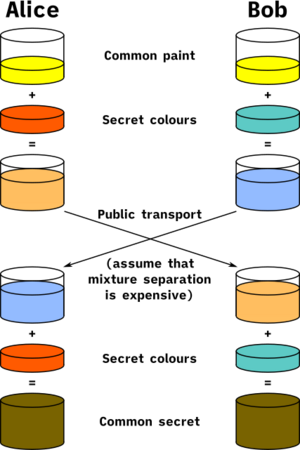
Let's imagine two friends, Alice and Bob, want to agree on a secret number. They can do this even if someone is listening to their conversation.
- Alice and Bob first agree on a public number. Let's say they choose 10. Everyone knows this number.
- Alice then chooses her own secret number. Let's say she picks 15. She keeps this number private.
- Alice adds her secret number to the public number: 10 + 15 = 25. She sends the result, 25, to Bob.
- Bob does the same thing. He chooses his own secret number, say 30. He keeps this private.
- Bob adds his secret number to the public number: 10 + 30 = 40. He sends the result, 40, to Alice.
Now, here's the clever part:
- Alice has Bob's result (40). She adds her own secret number (15) to it: 40 + 15 = 55.
- Bob has Alice's result (25). He adds his own secret number (30) to it: 25 + 30 = 55.
Both Alice and Bob end up with the same secret number, 55. No one else listening knows their secret numbers (15 and 30). This means a spy can't figure out the final secret number (55) just by listening to the numbers Alice and Bob sent (25 and 40). This is because the spy doesn't know the private numbers (15 and 30) that were added.
This method is very useful in computer security. Computers use very large numbers and complex math. This makes it almost impossible for someone to guess the secret numbers. It stops people from trying to "brute force" or guess every possible number until they find the right one.
Potential Problems and How to Stay Safe
While Diffie-Hellman is very useful, it can have a weakness called a "man-in-the-middle attack." This happens because Alice and Bob don't have to prove who they are before they start sharing numbers.
Imagine a sneaky person, Charlie, who pretends to be Bob when talking to Alice, and pretends to be Alice when talking to Bob. Charlie could trick both of them into sharing their secret numbers with him instead of with each other. Then, Charlie would know both Alice's and Bob's secret numbers.
To prevent this, people often use something called authentication. This means Alice and Bob take extra steps to prove their identity to each other before they start the Diffie-Hellman exchange. This way, they know they are talking to the right person and not a trickster like Charlie.
Related Topics to Explore
- Public-key cryptography
- Key-agreement protocol
- Password-authenticated key agreement
See also
 In Spanish: Diffie-Hellman para niños
In Spanish: Diffie-Hellman para niños