Formal fallacy facts for kids

A formal fallacy is a mistake in how an argument is built. It's like having a puzzle where the pieces don't fit together correctly, even if each piece looks fine on its own. In logic, this means an argument's conclusion doesn't necessarily follow from its starting points, called premises, because of a flaw in its structure.

Imagine you have a set of rules for a game. A formal fallacy happens when someone breaks those rules, even if they use true facts. The argument might have true facts, but the way they are connected is wrong. This means the conclusion might not be true, or it might be true by accident, not because the argument proves it.

Sometimes, a formal fallacy is called a deductive fallacy or a logical fallacy. Another term is "non sequitur," which is Latin for "it does not follow." This term is often used for mistakes in arguments that don't have a specific name.

A special kind of formal fallacy is a mathematical fallacy. This is an intentionally wrong mathematical proof. People often create these to teach others about common mistakes in math.

Formal fallacies are different from informal fallacies. An informal fallacy might have a correct structure, but its facts (premises) might be false. A formal fallacy, however, is wrong because of its structure, even if the facts are true.

What are Formal Fallacies?

Formal fallacies are errors in the logical structure of an argument. Think of it like a recipe. If you mix the ingredients in the wrong order, the cake might not turn out right, even if you used all the correct ingredients.

Even if an argument has a formal fallacy, its facts or conclusion might still be true. But the argument itself doesn't prove the conclusion. For example, someone might use a bad argument to say the sky is blue. The sky is blue, but their argument didn't prove it correctly.

Affirming the Consequent

This is a common mistake in arguments. It looks like this:

• If A is true, then B is true.
• B is true.
• Therefore, A is true.

Let's use an example:

• If Jackson is a human, then Jackson is a mammal.
• Jackson is a mammal.
• Therefore, Jackson is a human.

The conclusion ("Jackson is a human") might be true. But it doesn't have to be true based on the argument. Jackson could be a mammal without being a human, like an elephant or a cat. The argument's structure is flawed.

Denying the Antecedent

This is another common formal fallacy. It follows this pattern:

• If A is true, then B is true.
• A is false.
• Therefore, B is false.

Here's an example:

• If I am Japanese, then I am Asian.
• I am not Japanese.
• Therefore, I am not Asian.

The conclusion ("I am not Asian") might be true. But it doesn't logically follow. The person could be Asian but from a different country, like China or Korea. The argument is still wrong, even if the conclusion happens to be true.

Affirming a Disjunct

This fallacy happens when "or" is used in a way that allows both options to be true. The pattern is:

• A or B is true.
• B is true.
• Therefore, A is not true.

Example:

• I am at home or I am in the city.
• I am at home.
• Therefore, I am not in the city.

The conclusion ("I am not in the city") might be true. But the argument is flawed because you could be both at home and in the city at the same time (for example, if your home is in the city). This fallacy only happens when "or" means "one or the other, or both." If "or" means "one or the other, but not both," then it's not a fallacy.

Denying a Conjunct

This fallacy happens when you incorrectly assume one thing must be true if another is false. The pattern is:

• It is not true that A and B are both true.
• B is not true.
• Therefore, A is true.

Example:

• I cannot be both at home and in the city.
• I am not at home.
• Therefore, I am in the city.

The conclusion ("I am in the city") might be true. But it doesn't logically follow. You could be neither at home nor in the city (for example, you could be on vacation somewhere else).

Illicit Commutativity

This fallacy incorrectly assumes that if one thing leads to another, then the reverse is also true. The pattern is:

• If A is true, then B is true.
• Therefore, if B is true, then A is true.

Example:

• If it is raining, then I have my umbrella.
• Therefore, if I have my umbrella, then it is raining.

The first statement means you use your umbrella when it rains. But it doesn't mean you *only* use your umbrella when it rains. You might have your umbrella on a sunny day just in case, or because you forgot to put it away. So, having your umbrella doesn't automatically mean it's raining.

Fallacy of the Undistributed Middle

This fallacy happens in arguments that compare groups of things. It looks like this:

• All Zs are Bs.
• Y is a B.
• Therefore, Y is a Z.

Let's use an example:

• All humans are mammals.
• Mary is a mammal.
• Therefore, Mary is a human.

The conclusion ("Mary is a human") might be true. But the argument doesn't prove it. Mary could be a mammal like a dog or a cat, not necessarily a human. The mistake is assuming that because humans are a type of mammal, anything that is a mammal must be a human.

Formal vs. Informal Fallacies

In logic, arguments can be either valid or invalid.

• A valid argument has a correct structure. If its starting facts (premises) are true, then its conclusion *must* be true.
• A sound argument is a valid argument that *also* has true starting facts.

Formal fallacies are about whether an argument is valid, meaning its structure is correct. They don't care if the facts themselves are true.

Let's look at a valid argument structure, called modus ponens:

• If P is true, then Q is true.
• P is true.
• Therefore, Q is true.

An example of this valid structure:

• If it rains, the street will be wet.
• It rained.
• Therefore, the street is wet.

If the first two statements are true, the third one *must* be true. This is a valid argument. If it actually rained, it would also be a sound argument.

Now, let's look at an argument with a formal fallacy, like affirming the consequent again:

• If P is true, then Q is true.
• Q is true.
• Therefore, P is true.

Example:

• If it rains, the street will be wet.
• The street is wet.
• Therefore, it rained.

The street could be wet for other reasons, like someone washing a car. So, even if the street is wet, it doesn't *have* to mean it rained. This argument has a formal fallacy because its structure is wrong.

Here's another example of a formal fallacy with true facts:

• If an animal is a dog, then it has four legs.
• My cat has four legs.
• Therefore, my cat is a dog.

Both statements 1 and 2 are true. But statement 3 does not follow logically. The argument makes a mistake in its structure, even though the facts are correct.

Common Examples

Here are some everyday examples of formal fallacies:

"Some of your main evidence is missing or even faked! That proves I'm right!" This argument is flawed. Even if someone's evidence is bad, it doesn't automatically mean the opposite person is right. There might be other reasons or other evidence.

"The vet can't find any good reason why my dog died. See! That proves you poisoned him! There’s no other logical explanation!" Just because the vet can't find a reason doesn't mean there's only one possible explanation (poisoning). There could be many unknown reasons.

Consider this argument:

• Most of the green things are touching the red things.
• Most of the red things are touching the blue things.
• Therefore, most of the green things must be touching the blue things.

An Euler diagram illustrating a fallacy:
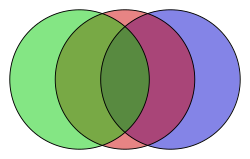
Statement 1: Most of the green is touching the red.
Statement 2: Most of the red is touching the blue.
Logical fallacy: Since most of the green is touching red, and most of the red is touching blue, most of the green must be touching blue. This, however, is a false statement.

This is a fallacy. Even if most green touches red, and most red touches blue, it doesn't guarantee that most green touches blue. Imagine a long chain: green-red-blue. The green might only touch the red, and the red might only touch the blue, with green and blue far apart.

Another example:

• All birds have beaks.
• That creature has a beak.
• Therefore, that creature is a bird.

This is a common mistake. While birds have beaks, other animals do too, like octopuses, squids, and some turtles. So, just because a creature has a beak doesn't mean it's a bird. The argument incorrectly assumes that if all birds have beaks, then all beaked creatures must be birds.

Non Sequitur in Everyday Speech

In daily conversations, a "non sequitur" can also mean a statement where the end part has nothing to do with the beginning. It's a sudden change of topic or a conclusion that seems completely out of place.

For example, from a book: "Life is life and fun is fun, but it's all so quiet when the goldfish die." The last part about the goldfish dying doesn't logically connect to the first part about life and fun.

See also