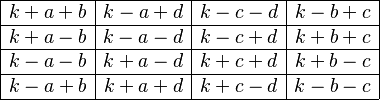Geometric magic square facts for kids

A geometric magic square, often called a geomagic square, is a special kind of puzzle invented by Lee Sallows in 2001. You might know about regular magic squares where numbers in rows, columns, and diagonals all add up to the same total. A geomagic square is similar, but instead of numbers, it uses geometric shapes!

In a geomagic square, the shapes in each row, column, or diagonal can be fitted together perfectly to make one special shape, called the target shape. Just like with number magic squares, all the shapes in a geomagic square must be different. Also, if you rotate or flip a square, it's still counted as the same square. The "dimension" of a geomagic square means if the pieces are flat (2D) or solid (3D). Most of the time, people study 2D squares with flat pieces.

Cool Examples of Geomagic Squares

Figure 1:   This geomagic square uses nine pieces that are all the same size.

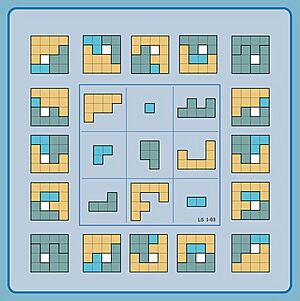
Figure 1 shows a 3 by 3 geomagic square. This means it has 3 rows and 3 columns. The 3 pieces in each row, column, and diagonal can be put together to form a rectangular target shape. You can see this target shape on the sides and top/bottom of the square. Here, all 9 pieces are "decominoes," which are shapes made of 10 connected squares.

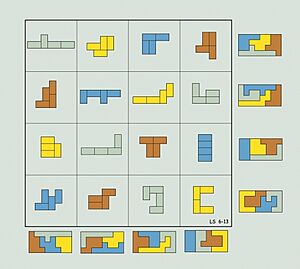
The pieces in a geomagic square don't have to be the same size. For example, in Figure 2, the pieces are "polyominoes" (shapes made of connected squares) that get bigger in size, from 1 unit up to 9 units. The target shape for these pieces is a 4 by 4 square with a hole in the middle.

Figure 2:   This geomagic square uses pieces of different sizes.

It's amazing to think that Figure 2 is just one of 4,370 different 3 by 3 geomagic squares that use pieces of these exact sizes and the same target shape! On the other hand, Figure 1, which uses pieces all the same size, is one of only two solutions. It seems that if the pieces are all the same size, there are fewer possible solutions. Scientists are still trying to figure out why this happens.

Figure 3:   This is a panmagic 3 by 3 geomagic square.

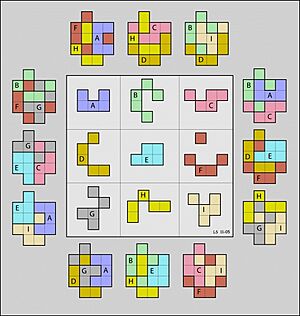
Sometimes, the pieces in a geomagic square can be "disjoint." This means they are made of separate parts, like islands. You can see an example in Figure 3. Because these pieces can overlap, they can sometimes fit together in ways that connected pieces cannot. This extra flexibility often allows geomagic squares to have special symmetries that number magic squares don't.

Geomagic squares can also be 3D! These squares use solid pieces that combine to form the same solid target shape. Figure 5 shows an example where the target shape is a cube.

How Geomagic Squares Are Made

It's not easy to create geomagic squares, except for very simple ones. So far, two main ways have been found to build them.

Using Computers to Search

If the pieces are "polyforms" (shapes made from many smaller, identical units), computers can search for solutions. For example, to create Figure 1, the first step is to decide on the size of the pieces (here, all the same) and the target shape. A computer program can then list every possible way to tile the target shape using 3 different decominoes. Each decomino is given a unique number.

Then, another part of the program tests every combination of three different groups of numbers. These groups are treated as the rows in a 3 by 3 square. The program then checks if the columns and diagonals also contain three numbers that are on the list of possible tilings. If they do, a geomagic square is found! If not, different target shapes can be tried. This method can be changed to search for larger squares or squares with pieces of different sizes.

Modifying Existing Squares

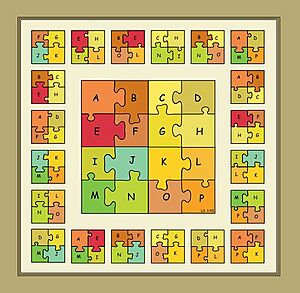
Another way to make geomagic squares starts with a simple one that has repeated pieces. Then, the shapes of these pieces are changed so they are all different, but without messing up the square's "magic" property. This is done using a special algebraic pattern, like the one below. The different letters in the pattern represent small shapes that are either added to or taken away from the original pieces.

Figure 4:   This is a 'self-interlocking' geomagic square.

Figure 4 shows how this works. Here, the letter k stands for a small square shape. The letters a, b, c, and d represent parts that are added (+) or removed (-) from the square. This process creates 16 unique jigsaw pieces that fit together perfectly.

How Geomagic Squares Relate to Number Magic Squares

It might seem like geomagic squares are just a type of magic square, but it's actually the other way around! Every regular (additive) magic square is a specific type of geomagic square, but not all geomagic squares are regular magic squares.

Let's look at an example from an article by Jean-Paul Delahaye in Pour la Science (the French version of Scientific American). In this example, the "target shape" for the geomagic square on the right is simply a one-dimensional line segment that is 15 units long. The "pieces" are just straight line segments. This shows how a regular number magic square (on the left) can be turned into a geomagic square using shapes.

As Delahaye explains, "This example shows that the geomagic square idea includes magic squares. The result here isn't very exciting, but luckily there are other geomagic squares that aren't just simple translations like this."

So, every number magic square can be seen as a one-dimensional geomagic square. Lee Sallows himself said, "Traditional magic squares with numbers are actually a special case of 'geomagic' squares where the pieces are all one-dimensional." But even in one dimension, there are geomagic squares with disconnected line segments that don't match any number magic square. This means that traditional magic squares are just a tiny part of all possible geometric magic squares.

Special Types of Geomagic Squares

Geomagic squares can have even more amazing "magic" properties than number magic squares.

Panmagic Squares

A panmagic square is one where every diagonal, including the "broken diagonals" (diagonals that wrap around the edges), also shares the same magic property as the rows and columns. It's impossible to make a 3 by 3 panmagic square with numbers. However, you can see a geometric example in Figure 3! So far, no one has found a similar example using connected pieces.

Figure 5:   This is a 3D geomagic square with cubic target shapes.

Figure 6:   This geomagic square's pieces can tile themselves.

Other Unique Properties

Besides being geomagic, some squares have extra cool features. For example, in Figure 6, the square is magic only on its rows and columns. But its 16 pieces form a "Self-tiling tile set." This means that each of the 16 different shapes can be tiled (covered) by smaller copies of the complete set of all 16 shapes.

Another special type is Figure 4, which is a "self-interlocking" geomagic square. Here, the 16 pieces are not just placed inside separate cells. Instead, they actually form the shapes of the square cells themselves, fitting together like a jigsaw puzzle to complete a large square.

Images for kids

• 

  Macau stamp featuring geometric magic square