Graham's number facts for kids
Graham's number is a super-duper big natural number. It was named after a mathematician called Ronald Graham. He used this number to help solve a tricky problem in a math area called Ramsey theory. Graham showed that the answer to his problem was actually smaller than this huge number.
Graham's number is one of the largest numbers ever used in a serious mathematical proof. It's so big that if you tried to write down every single digit, even in the tiniest handwriting, it would be too large to fit inside the entire observable universe!
What is Ramsey Theory?
Ramsey theory is a part of math that asks interesting questions about patterns. Imagine you have a group of friends. If some are connected by a red line (meaning they like each other) and some by a blue line (meaning they don't), can you always find a group of 3 friends where all their connections are the same color?
For a simple example:
Imagine you draw some points, and connect every pair of points with a line. Some lines are blue and some are red. Can you always find 3 points where the 3 lines connecting them are all the same color?
It turns out that if you have 6 or more points, the answer is always "yes"! No matter how you color the lines, you'll find a group of 3 points with all same-colored lines. But if you have 5 points or fewer, you can color the lines so that this doesn't happen.
Graham's number comes from a much harder version of this question.
Again, imagine you have points, but this time they are the corners of an n-dimensional hypercube. All these points are still connected by blue and red lines. For any 4 points, there are 6 lines connecting them. Can you find 4 points that all lie on one flat surface, and all 6 lines connecting them are the same color?
Asking that the 4 points lie on a flat surface makes the problem much more difficult. We want to know: for which values of n is the answer "no" (meaning you can avoid the pattern), and for which values of n is it "yes" (meaning the pattern always appears)? This problem hasn't been fully solved yet.
In 1971, Ronald Graham and B. L. Rothschild found a partial answer. They showed that for n=6, the answer is "no". But when n is very, very large, like Graham's number or even bigger, the answer is "yes".
This partial answer was important because it proved that the pattern eventually *does* appear for some very large n. Before 1971, mathematicians didn't even know that much!
How to Define Graham's Number
Graham's number is so incredibly huge that you can't even write it using normal scientific notation. To write it down, we need a special way called Knuth's up-arrow notation.
Let's look at some examples of how up-arrows work:
means 3 multiplied by itself 3 times. So, 3 × 3 × 3 = 27.
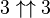is like saying 
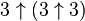. Since Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 3 \uparrow 3 is 27, this means 3 with 27 arrows. So, 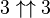means 3 multiplied by itself 27 times. That equals 7,625,597,484,987.
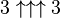means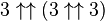 
. We know 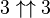is 7,625,597,484,987. So, this is 3 with two arrows, repeated 7,625,597,484,987 times. This number is so big that its digits, even written tiny, would fill up the entire observable universe and beyond!
- Even though this number is already beyond what we can imagine, this is just the beginning of how Graham's number is built.
- The next step like this is
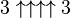. This is the number we will call g1.
Now, we will define a sequence of numbers: g1, g2, g3, and so on. Each number helps define the next.
- g1 is 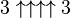(which has 4 arrows).
- g2 is
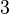with a number of arrows equal to g1. Imagine writing 3, then an arrow, then 3, and you keep adding arrows until you have g1 arrows in total. - g3 is 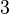with a number of arrows equal to g2.
We keep going like this, making the number of arrows grow incredibly fast. We stop when we define g64.
g64 is 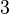with a number of arrows equal to g63.
This final number, g64, is Graham's number. It's truly one of the biggest numbers ever used in a mathematical proof!
Related pages
See also
In Spanish: Número de Graham para niños
