Graph (mathematics) facts for kids
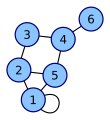
In math, a graph is a special way to show how different things are connected. Think of it like a map where cities are points and roads are lines connecting them. These points are called vertices (say "VER-tih-sees"), and the connections between them are called edges. Graphs help us understand relationships, like how friends are connected on social media or how computers are linked in a network.
Contents
What are Graphs?
A graph is made up of two main parts:
- Vertices: These are the individual items or points in your graph. You can think of them as dots.
- Edges: These are the connections or lines between the vertices. They show how the items are related.
If two vertices are connected by an edge, we say they are adjacent. It just means they are neighbors in the graph.
How Many Connections?
The degree of a vertex tells you how many edges are connected to it. For example, if a city has three roads leading out of it, that city's vertex has a degree of three.
The size of a graph is simply the total number of edges it has. The order of a graph is the total number of vertices.
What are Edge Weights?
Sometimes, edges can have weights. A weight is like a cost or a value associated with using that connection.
- For a map of cities, the weight could be the distance between two cities.
- It could also be the time it takes to travel from one city to another.
- In a computer network, it might be the speed of the connection.
These weights help us find the best path, like the shortest or fastest route.
Types of Graphs
Graphs come in different types, depending on how their edges work.
Directed and Undirected Graphs
- Directed graphs have edges that only go in one direction. Imagine a one-way street or water flowing through a pipe. You can only travel along the edge in the direction of the arrow.
- Undirected graphs have edges that go both ways. Think of a two-way street or a mutual friendship. If person A is friends with person B, then person B is also friends with person A.
Simple and Multigraphs
- A simple graph is a graph where there is at most one edge between any two vertices. Also, no vertex is connected to itself.
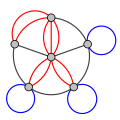
- A multigraph allows more than one edge between the same two vertices. Imagine two different roads connecting the same two cities. A multigraph can also have a loop, which is an edge that connects a vertex to itself.
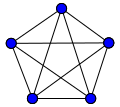
Complete Graphs
A complete graph is a special type of simple graph. In a complete graph, every single vertex is directly connected to every other vertex. It's like everyone in a small group is friends with everyone else.
Paths and Cycles
- A path is a sequence of edges that takes you from one vertex to another. Think of it as a journey through the graph.
- A cycle is a path that starts and ends at the same vertex. It's like taking a trip and ending up right back where you started.
Images for kids