Hoffman's packing puzzle facts for kids
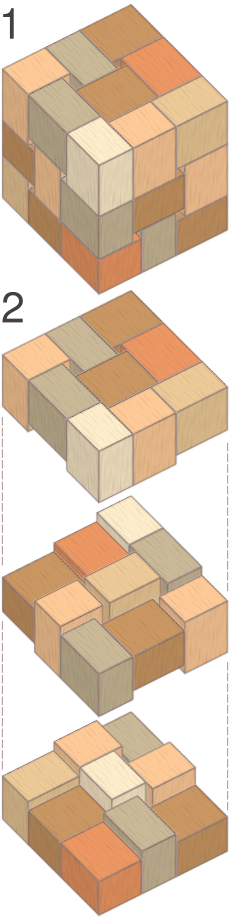
The Hoffman's packing puzzle is a fun assembly puzzle. It was named after Dean G. Hoffman, who first talked about it in 1978. This puzzle uses 27 identical blocks, which are shaped like long rectangles called cuboids. Each block has three different side lengths.
The main goal of the puzzle is to fit all 27 of these blocks perfectly into a single large cube. The side length of this big cube is found by adding up the three different side lengths of one small block. The first person to solve this puzzle was David A. Klarner. People usually take anywhere from 20 minutes to several hours to solve it!
What is Hoffman's Packing Puzzle?
This puzzle is made up of 27 identical rectangular blocks. Most physical versions of the puzzle also come with a cube-shaped box. You need to fit all the blocks into this box.
Let's say the three different side lengths of one block are called x, y, and z. Then, the big cube you need to fill will have a side length of x + y + z.
Making the Puzzle Harder
You can make this puzzle using any three different side lengths for the blocks. However, it becomes much harder when the three side lengths are very similar. This is because it stops you from using simpler ways to solve it.
It also gets more confusing if the three lengths are part of an arithmetic progression. This means the lengths increase by the same amount each time (like 2, 4, 6). In this case, if you line up three blocks of the middle length, they might look like they fit. But this arrangement won't lead to a correct solution for the whole puzzle.
Solving in Different Dimensions
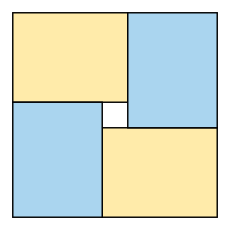
Imagine a simpler version of this puzzle in two dimensions. This would be like trying to fit four identical rectangles into a larger square. If the rectangle's sides are x and y, the square would have sides of x + y. As you can see in the picture, this is always possible to solve.
In higher dimensions, the puzzle asks you to pack many identical blocks into a hypercube. For example, in four dimensions, you'd pack 4x4x4x4 (256) blocks!
A mathematician named Raphael M. Robinson found that this puzzle can be solved in many dimensions. For example, it's solvable in 4, 6, 8, and 9 dimensions. However, we don't know if it can be solved in five dimensions or other prime number dimensions (like 7 or 11).