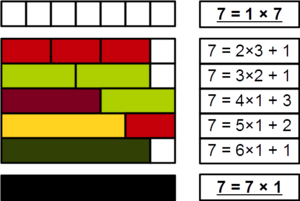
Prime number facts for kids

"Prime" redirects here. For other uses, see Prime (disambiguation).

A prime number is a special natural number (like 1, 2, 3, 4, and so on) that is greater than 1. What makes it special? It can only be divided evenly by two numbers: 1 and itself. Think of it as a number that can't be broken down into smaller multiplication pairs.

If a number greater than 1 is not prime, we call it a composite number. For example, 5 is a prime number because you can only make 5 by multiplying 1 × 5 or 5 × 1. But 4 is a composite number because you can make it by multiplying 2 × 2, where both 2s are smaller than 4.

Prime numbers are super important in math, especially in a field called number theory. They are like the basic "building blocks" for all other whole numbers (greater than 1). This is because every whole number larger than 1 is either a prime itself, or it can be uniquely broken down into a product of prime numbers. This is called the fundamental theorem of arithmetic.

The idea of a number being prime is called primality. There are ways to check if a number is prime, like trying to divide it by smaller numbers. Faster methods exist, some that are very quick but might have a tiny chance of error, and others that are slower but always correct. As of October 2024, the largest known prime number has over 41 million digits!

There are endless prime numbers. This was proven by a Greek mathematician named Euclid a very long time ago, around 300 BC. Even though there are infinitely many, there isn't a simple formula to find them all or tell them apart from composite numbers easily.

Prime numbers are not just for math class! They are used in many real-world technologies. For example, they are key to keeping your online information safe through public-key cryptography. This technology relies on how hard it is to break down very large numbers into their prime factors.

What Are Prime Numbers?

A natural number (like 1, 2, 3, 4, 5, 6, etc.) is called a prime number if it's bigger than 1 and cannot be made by multiplying two smaller natural numbers. Numbers greater than 1 that are not prime are called composite numbers.

Imagine you have a certain number of dots. If you can arrange these dots into a rectangle that is more than one dot wide and more than one dot high, then the number is composite. If you can only arrange them in a single line (1 dot wide or 1 dot high), then it's a prime number!

For example, let's look at numbers from 1 to 6:

1 is not prime (it's a special case).
2 is prime (only 1 × 2).
3 is prime (only 1 × 3).
4 is composite (2 × 2).
5 is prime (only 1 × 5).
6 is composite (2 × 3).

Demonstration, with Cuisenaire rods, that 7 is prime, because none of 2, 3, 4, 5, or 6 divide it evenly

Every natural number has 1 and itself as divisors (numbers that divide it evenly). If a number has any other divisors, it's not prime. So, prime numbers are numbers with exactly two positive divisors: 1 and the number itself. This is why 1 is not prime; it only has one divisor (itself).

The first 25 prime numbers (all the primes less than 100) are:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97 (sequence A000040 in OEIS).

Did you notice something? No even number greater than 2 is prime. Why? Because any even number can be divided by 2! So, 2 is the only even prime number. All other primes are odd numbers, and we call them odd primes. Also, prime numbers larger than 5 always end in 1, 3, 7, or 9. Numbers ending in 0, 2, 4, 6, or 8 are even, and numbers ending in 0 or 5 are divisible by 5.

A Look Back: History of Primes

The Rhind Mathematical Papyrus

People have been studying prime numbers for a very long time! The Rhind Mathematical Papyrus, an ancient Egyptian text from around 1550 BC, shows some early ideas about numbers. However, the first clear records of studying prime numbers come from ancient Greek mathematicians.

Around 300 BC, the famous Greek mathematician Euclid wrote a book called Elements. In it, he proved that there are infinitely many prime numbers. He also showed how every number can be broken down into a unique set of prime factors. Another Greek invention, the Sieve of Eratosthenes, is still used today to find lists of prime numbers.

Later, around 1000 AD, Islamic mathematicians like Ibn al-Haytham (also known as Alhazen) and Ibn al-Banna' al-Marrakushi made more discoveries. Ibn al-Haytham found a way to describe prime numbers using factorials. Ibn al-Banna' al-Marrakushi improved the Sieve of Eratosthenes to make it faster.

In the 13th century, Fibonacci brought many of these mathematical ideas from the Islamic world to Europe. His book Liber Abaci (1202) was the first to explain a method called trial division for checking if a number is prime.

Over the centuries, many brilliant mathematicians, like Pierre de Fermat, Marin Mersenne, Christian Goldbach, and Leonhard Euler, continued to explore the mysteries of prime numbers. They discovered new theorems, made educated guesses (called conjectures), and developed new ways to understand how primes are distributed.

In the 1970s, something big happened. Prime numbers, which were once seen as just "pure math" with no real-world uses, became super important for public-key cryptography. This led to a lot more research into how to find and use prime numbers with computers.

Why 1 Is Not a Prime Number

For a long time, mathematicians debated whether the number 1 should be considered a prime number. Some early lists of primes even included it! However, by the early 20th century, mathematicians generally agreed that 1 should not be called prime.

Why the change? If 1 were prime, many important math rules and theorems about primes would become much more complicated. For example, the fundamental theorem of arithmetic, which says every number has a unique prime factorization, wouldn't be true anymore. You could factor 6 as 2 × 3, or 1 × 2 × 3, or 1 × 1 × 2 × 3, and so on, making the factorization not unique.

Also, the sieve of Eratosthenes (a method to find primes) wouldn't work correctly if 1 was prime. It would eliminate all other numbers! So, to keep mathematical rules simple and consistent, 1 is now considered a special number called a "unit," not a prime.

Basic Features of Primes

Unique Prime Building Blocks

Breaking down a number into its prime factors is called prime factorization. It's like finding the unique set of prime "building blocks" that multiply together to make that number.

For example:

50 can be written as 2 × 5 × 5.
We can also write this as 2 × 5² (meaning 2 times 5 squared).

The numbers in this product (2 and 5) are called prime factors. Even if a prime factor appears more than once, it's still part of the unique set.

The fundamental theorem of arithmetic tells us that every whole number larger than 1 can be written as a product of one or more primes. And the amazing part is that this product is always unique! No matter how you find the factors, you'll always end up with the same prime numbers, just maybe in a different order. This is why primes are considered the basic building blocks of natural numbers.

Endless Primes

There are infinitely many prime numbers. This means the list of primes (2, 3, 5, 7, 11, 13, ...) never ends! This idea is known as Euclid's theorem, named after the ancient Greek mathematician.

Euclid's proof is quite clever. Imagine you have a list of all the prime numbers you can think of. Euclid showed that you can always find a new prime number that isn't on your list. How?

1. Multiply all the primes on your list together. 2. Add 1 to that huge product. Let's call this new number N. 3. Now, N must either be a prime number itself, or it must have prime factors (its own building blocks). 4. If N is prime, then you've found a new prime not on your original list! 5. If N is composite, it must be divisible by some prime number. But if you try to divide N by any of the primes on your original list, you'll always get a remainder of 1. This means N's prime factors cannot be any of the primes on your list. So, N must have a prime factor that is *not* on your list.

Either way, you always find a new prime! This shows that no matter how many primes you list, there will always be more.

No Simple Formulas for Primes

Many people have tried to find a simple formula that only produces prime numbers. However, no one has found an easy formula that works every time. For example, there's no simple math rule that can generate *only* prime numbers for every input.

Some formulas can produce primes for a while, but eventually, they start giving composite numbers. This means finding primes often requires checking numbers one by one or using more complex methods.

Unsolved Prime Puzzles

Even with all the study, there are still many big mysteries about prime numbers that mathematicians haven't solved! These are called conjectures. Here are a couple of famous ones:

Goldbach's Conjecture: This idea says that every even number greater than 2 can be written as the sum of two prime numbers. For example, 4 = 2 + 2, 6 = 3 + 3, 8 = 3 + 5, 10 = 3 + 7 (or 5 + 5). This has been checked for incredibly large numbers, but no one has proven it's true for *all* even numbers.
Twin Prime Conjecture: Twin primes are pairs of prime numbers that are only 2 apart, like (3, 5), (5, 7), (11, 13), (17, 19). This conjecture suggests that there are infinitely many such pairs. Again, mathematicians have found many twin primes, but they haven't proven that the list never ends.

These unsolved puzzles keep mathematicians busy and lead to new discoveries in number theory!

How Many Primes Are There?

The relative error of

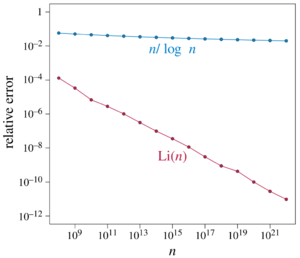
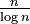\tfrac{n}{\log n}

as an approximation to the prime-counting function. The error decreases to zero as

n

grows.

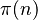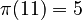The prime-counting function, written as $\pi(n)$ , tells us how many prime numbers there are up to a certain number $n$ . For example, $\pi(11)=5$ because the primes less than or equal to 11 are 2, 3, 5, 7, and 11.

The prime number theorem gives us a good estimate for how many primes there are as numbers get very large. It says that the number of primes up to $n$ is roughly equal to $n$ divided by the natural logarithm of $n$ . This means that as numbers get bigger, primes become less common, but they never truly run out.

Primes in Patterns

An arithmetic progression is a sequence of numbers where the difference between consecutive numbers is always the same. For example, 3, 12, 21, 30, 39... is an arithmetic progression where each number is 9 more than the last.

If the starting number and the common difference of an arithmetic progression don't share any common factors (other than 1), then Dirichlet's theorem on arithmetic progressions says that the progression will contain infinitely many prime numbers!

Even more amazing, the Green–Tao theorem shows that you can find arithmetic progressions of primes that are as long as you want. For example, you can find a sequence of 3 primes, or 4 primes, or 100 primes, all equally spaced apart!

The Ulam spiral. Prime numbers (orange) cluster on some diagonals.

The Ulam spiral is a cool way to visualize prime numbers. If you write numbers in a spiral pattern and highlight the primes, you'll notice that primes tend to line up along certain diagonal lines. This suggests that some simple math rules might produce primes more often than others, but it's still a mystery why.

Computer Power and Primes

For a long time, prime numbers were mostly a topic for pure mathematicians. But in the 1970s, everything changed when it was discovered that primes could be used to create secure public-key cryptography systems. This made finding and working with prime numbers a very important task for computers.

Checking if a Number Is Prime

The simplest way to check if a number $n$ is prime is called trial division. You try dividing $n$ by every whole number starting from 2, up to the square root of $n$ . If any of these numbers divide $n$ evenly (with no remainder), then $n$ is composite. If none of them do, then $n$ is prime.

For example, to check if 37 is prime, you'd try dividing it by 2, 3, 4, 5, and 6 (since the square root of 37 is about 6.08). Since 37 isn't evenly divisible by any of these, it's prime!

This method works, but it's too slow for very large numbers. Modern computers use much faster methods.

Finding Many Primes with Sieves

The sieve of Eratosthenes starts with all numbers unmarked. It repeatedly finds the first unmarked number, marks it as prime, and marks its multiples as composite.

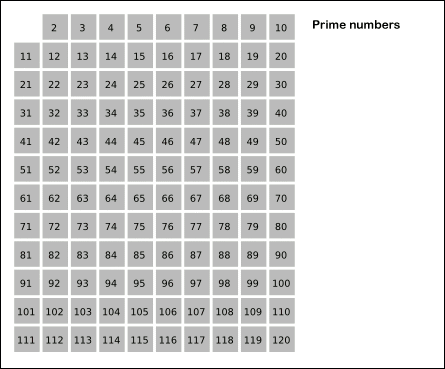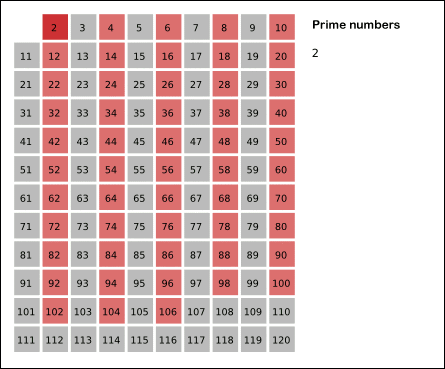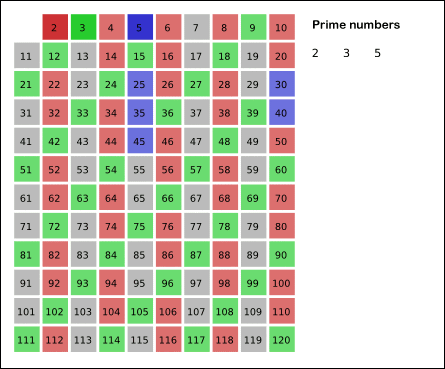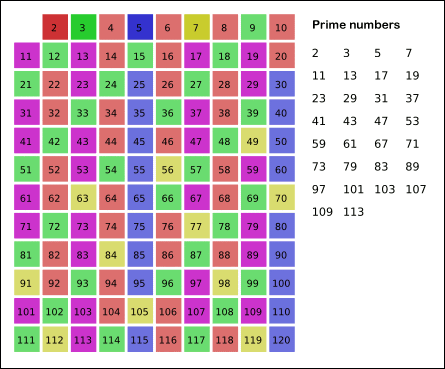
Before computers, people made lists of primes by hand. The oldest method for this is the sieve of Eratosthenes. It works like this: 1. Write down all the numbers up to a certain limit. 2. Start with 2 (the first prime). Circle 2, then cross out all its multiples (4, 6, 8, etc.). 3. Move to the next uncrossed number, which is 3. Circle 3, then cross out all its multiples (6, 9, 12, etc.). 4. Continue this process. The numbers that remain circled and uncrossed are the prime numbers!

The Biggest Primes We Know

Thanks to powerful computers and special algorithms, mathematicians keep finding bigger and bigger prime numbers. The Lucas–Lehmer primality test is especially good at finding a type of prime called a Mersenne number (primes that are one less than a power of two). This is why the largest known prime has almost always been a Mersenne prime since 1992.

As of October 2024, the largest known prime number is 2^136,279,841 − 1. This number is so huge it has 41,024,320 decimal digits! It was discovered by Luke Durant as part of the Great Internet Mersenne Prime Search (GIMPS) project, which uses many computers around the world working together.

Here are some of the largest known primes of different types:

Type	Prime	Number of decimal digits	Date	Found by
Mersenne prime	2^136,279,841 − 1	41,024,320	October 12, 2024	Luke Durant, Great Internet Mersenne Prime Search
Proth prime	10,223 × 2^31,172,165 + 1	9,383,761	October 31, 2016	Péter Szabolcs, PrimeGrid
factorial prime	208,003! − 1	1,015,843	July 2016	Sou Fukui
primorial prime	1,098,133# − 1	476,311	March 2012	James P. Burt, PrimeGrid
twin primes	2,996,863,034,895 × 2^1,290,000 ± 1	388,342	September 2016	Tom Greer, PrimeGrid

Breaking Numbers Apart: Factorization

Finding the prime factors of a composite number is called factorization. This is much harder than just checking if a number is prime. While there are many factorization algorithms, they are generally slower than primality tests.

The difficulty of factoring very large numbers is what makes many modern security systems work. For example, the RSA encryption system relies on the fact that it's easy to multiply two large prime numbers together, but incredibly difficult to figure out those two original primes if you only have their product.

Primes in Everyday Tech

The small gear in this piece of farm equipment has 13 teeth, a prime number.

Prime numbers are used in many parts of computer science:

Cryptography: As mentioned, they are essential for keeping online communications and data secure.
Hash Tables: These are data structures used in computers to store and quickly retrieve information. Using prime numbers for certain sizes or calculations helps them work more efficiently.
Checksums: These are codes used to check for errors in data. For example, the numbers in International Standard Book Numbers (ISBNs) use a calculation involving the prime number 11 to detect mistakes.
Random Numbers: Prime numbers are also used in creating pseudorandom number generators, which are algorithms that produce sequences of numbers that appear random, useful for simulations and games.

Primes Beyond Math

Prime numbers pop up in surprising places, even outside of pure mathematics and computing.

Shapes and Primes

Construction of a regular pentagon using straightedge and compass. This is only possible because 5 is a Fermat prime.

Did you know that prime numbers are connected to drawing shapes? A regular polygon (a shape with equal sides and angles) can be drawn perfectly using only a straightedge and compass if its number of sides has special prime factors called Fermat primes. For example, a 5-sided pentagon can be drawn this way because 5 is a Fermat prime.

Nature's Primes

In the natural world, some insects called cicadas use prime numbers in their life cycles! These insects spend most of their lives underground as grubs. They only come out to breed after 7, 13, or 17 years. Biologists think these prime-numbered cycles help them avoid predators. If a predator had a life cycle that was a multiple of, say, 2 or 3 years, it would be harder for them to sync up with the cicadas' prime-numbered cycles.

Primes in Art and Stories

Prime numbers have even inspired artists and writers!

The French composer Olivier Messiaen used prime numbers in his music to create unique and unpredictable rhythms.
In the science fiction novel Contact by Carl Sagan, scientists try to communicate with aliens using prime numbers as a universal language.
The novel The Curious Incident of the Dog in the Night-Time uses prime numbers to number its chapters, reflecting the main character's mathematical mind.
In the novel The Solitude of Prime Numbers, primes are used as a metaphor for loneliness, portraying them as "outsiders" among other numbers.

Images for kids

Plot of the absolute values of the zeta function, showing some of its features
All Gaussian primes with norm squared less than 500