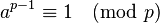kids encyclopedia robot

Fermat's primality test facts for kids

Kids Encyclopedia Facts

Fermat's primality test is a special algorithm. It helps us check if a number is likely a prime number. A prime number can only be divided evenly by 1 and itself (like 2, 3, 5, 7). This test is pretty good, but it has a small problem. Some numbers can pass the test even if they are not truly prime. These tricky numbers are called Carmichael numbers.

How the Test Works

This test uses a cool math rule called Fermat's little theorem. This theorem says that if a number p is prime, and you pick any number a that is smaller than p (but not zero), then this equation will always be true:

a^{p-1} \equiv 1 \pmod{p}

Testing a Number

To use this test, you pick a number n that you want to check. Then, you choose different random numbers for a. You plug n and a into the equation from Fermat's little theorem.

  • If the equation is NOT true for any a you pick, then n is definitely a composite number. A composite number is one that can be divided evenly by more than just 1 and itself (like 4, 6, 8, 9).
  • If the equation IS true for many different a values, then n is probably a prime number. We might call it a "pseudoprime" because it acts like a prime number in this test.

Fermat Liars and Witnesses

Sometimes, a number n might not be prime, but it still makes the equation true for some a values.

  • If n is a composite number, but it makes the equation 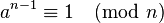a^{n-1} \equiv 1 \pmod{n} true, then a is called a Fermat liar. It "lies" about n being prime.
  • If you pick an a and the equation 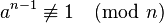a^{n-1} \not\equiv 1 \pmod{n} is NOT true, then a is called a Fermat witness. This a "witnesses" that n is definitely a composite number.

Understanding Modulo

The symbol 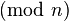\pmod n means "modulo n". It's a math operation that finds the remainder when one number is divided by another. For example, 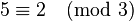Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 5 \equiv 2 \pmod 3 means that when you divide 5 by 3, the remainder is 2.

What This Test Is Used For

Fermat's primality test is useful in cryptography. Cryptography is the science of keeping information secret and secure. The RSA algorithm, which is used for public-key encryption, can use this test. Public-key encryption helps make sure your online messages and data are safe from prying eyes.

Images for kids

  • Kids robot

    A robot representing technology and learning.

kids search engine
All content from Kiddle encyclopedia articles (including the article images and facts) can be freely used under Attribution-ShareAlike license, unless stated otherwise. Cite this article:
Fermat's primality test Facts for Kids. Kiddle Encyclopedia.