Fermat's little theorem facts for kids

Fermat's Little Theorem is an important idea in number theory. It was discovered by a French mathematician named Pierre de Fermat in the 1600s. This theorem helps us understand special properties of prime numbers.

It basically says that if you pick any whole number, let's call it a, and any prime number, let's call it p, then when you multiply a by itself p times (which is written as a^p), the result will behave a lot like a itself when you divide it by p.

In math language, it looks like this:

Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): a^p \equiv a\,(\mathrm{mod}\,p)

This means that a^p and a leave the same remainder when divided by p.

There's also another common way to use this theorem. If a is not a multiple of p (meaning p doesn't divide a perfectly), then:

This means that a^p-1 will always leave a remainder of 1 when divided by p. This version is often used in computer science and cryptography!

Who Was Pierre de Fermat?

Pierre de Fermat was a brilliant French mathematician.

Pierre de Fermat was a French lawyer and mathematician. He lived from 1601 to 1665. Even though he was a lawyer, he spent a lot of his free time studying math. He made many important discoveries in different areas of mathematics. These included number theory, calculus, and probability.

Fermat is famous for several theorems. One of his most well-known is "Fermat's Last Theorem." This one took over 350 years for mathematicians to finally prove! Fermat's Little Theorem is much simpler to prove and use. It is still very useful today.

What Are Prime Numbers?

To understand Fermat's Little Theorem, you need to know about prime numbers. A prime number is a whole number greater than 1. It can only be divided evenly by two numbers: 1 and itself.

• Examples of prime numbers are 2, 3, 5, 7, 11, 13, and so on.
• The number 4 is not prime because it can be divided by 1, 2, and 4.
• The number 6 is not prime because it can be divided by 1, 2, 3, and 6.

Prime numbers are like the basic building blocks for all other whole numbers. Every whole number (greater than 1) can be made by multiplying prime numbers together.

Understanding Modular Arithmetic

Fermat's Little Theorem uses something called "modular arithmetic". This is sometimes called "clock arithmetic." It's a system of arithmetic for integers. Numbers "wrap around" when they reach a certain value. This value is called the modulus.

Think about a clock. If it's 10 o'clock and you add 4 hours, it's not 14 o'clock. It's 2 o'clock. This is because a clock works "modulo 12." We divide by 12 and look at the remainder.

In the theorem, 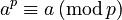Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): a^p \equiv a\,(\mathrm{mod}\,p) means:

• When you divide a^p by p, you get a certain remainder.
• When you divide a by p, you get a certain remainder.
• The theorem says these two remainders are the same!

Let's try an example:

• Let a = 2 and p = 5 (which is a prime number).
• The theorem says 2⁵ 2 (mod 5).
• 2⁵ = 2 x 2 x 2 x 2 x 2 = 32.
• If you divide 32 by 5, the remainder is 2 (because 32 = 5 x 6 + 2).
• If you divide 2 by 5, the remainder is 2.
• Since both remainders are 2, the theorem holds true!

Now let's try the second form: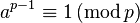

• Using a = 2 and p = 5 again.
• The theorem says 2^(5-1) 1 (mod 5), which is 2⁴ 1 (mod 5).
• 2⁴ = 2 x 2 x 2 x 2 = 16.
• If you divide 16 by 5, the remainder is 1 (because 16 = 5 x 3 + 1).
• So, this form also holds true!

Why Is It Important?

Fermat's Little Theorem is very useful in many areas:

• Cryptography: It helps create secure codes for online communication. This keeps your messages and information safe.
• Primality Testing: It can help check if a very large number is a prime number. This is important for many computer algorithms.
• Number Theory: It's a basic building block for understanding more complex ideas about numbers.

It's a simple yet powerful theorem that shows the amazing patterns hidden within numbers!

See also

In Spanish: Pequeño teorema de Fermat para niños