Number theory facts for kids
Number theory is a fascinating part of mathematics that studies numbers. It looks at different kinds of numbers, like prime numbers, and explores their special features. This field helps us understand how numbers work and how they can be used in real life.
Number theory is sometimes called the "Queen of Mathematics" because it deals with the most basic building blocks of math: numbers themselves!
Contents
What Does Number Theory Study?
Number theory explores many interesting ideas about numbers. Here are some of the main topics:
Prime Numbers
Prime numbers are super important in number theory. A prime number is a whole number greater than 1 that can only be divided evenly by 1 and itself. Examples are 2, 3, 5, 7, 11, and so on. Number theorists spend a lot of time trying to understand these special numbers.
Factorization
Factorization is about breaking down a number into its prime factors. For example, the number 12 can be factored into 2 × 2 × 3. This process is like finding the prime "ingredients" that make up a number. It's a key idea in understanding how numbers are built.
Other Types of Numbers
Number theory also looks at other types of numbers, like integers (whole numbers, positive, negative, or zero) and rational numbers (numbers that can be written as a fraction). It even touches on more complex ideas like matrices, which are grids of numbers used in many areas of math and science.
Important Discoveries in Number Theory
Over hundreds of years, mathematicians have made amazing discoveries in number theory. Here are a few famous ones:
The Fundamental Theorem of Arithmetic
This theorem is a basic rule in number theory. It says that every whole number greater than 1 can be written as a unique product of prime numbers. It's like saying every number has its own unique prime "fingerprint." For example, 30 is always 2 × 3 × 5, and you can't get 30 by multiplying a different set of prime numbers.
Fermat's Last Theorem
Fermat's Last Theorem was a very famous problem that puzzled mathematicians for over 350 years! It was first proposed by the French mathematician Pierre de Fermat in 1637. The theorem states that there are no three positive whole numbers a, b, and c that can satisfy the equation aⁿ + bⁿ = cⁿ for any whole number value of n greater than 2. It was finally proven by Andrew Wiles in 1994.
Chinese Remainder Theorem
The Chinese remainder theorem helps solve problems where you need to find a number that leaves specific remainders when divided by different numbers. Imagine you have a secret number, and you know that when you divide it by 3, the remainder is 1, and when you divide it by 5, the remainder is 2. This theorem helps you find that secret number!
Fermat's Little Theorem
Fermat's little theorem is another important result from Pierre de Fermat. It deals with how numbers behave when raised to a power and then divided by a prime number. This theorem is very useful in areas like cryptography, which is about secure communication.
How Number Theory is Used Today
Number theory might seem like an old subject, but it's super important in our modern world!
Encrypted Messaging
One of the most well-known uses of number theory is in encryption, which is used for secure messaging. When you send a text or email, or when you use online banking, number theory helps keep your information safe and private. Complex calculations involving prime numbers make it very hard for anyone else to read your messages. This is called public-key cryptography.
Data Compression
Number theory also plays a role in data compression. This is the process of making digital files smaller so they take up less space and can be sent faster. Think about how you can send photos or videos quickly over the internet – number theory helps make that possible!
Images for kids
-
The distribution of prime numbers is a central point of study in number theory. This Ulam spiral serves to illustrate it.
-
The Plimpton 322 tablet, an ancient Babylonian clay tablet that shows advanced knowledge of number theory.
-
Title page of the 1621 edition of Diophantus's Arithmetica, a very old book about numbers.
-
Al-Haytham as seen by the West: on the frontispiece of Selenographia Alhasen [sic] represents knowledge through reason and Galileo knowledge through the senses.
-
.
Pierre de Fermat, a French mathematician who made many important discoveries in number theory.
-
Leonhard Euler, a Swiss mathematician who contributed greatly to many areas of mathematics, including number theory.
-
"Here was a problem, that I, a 10 year old, could understand, and I knew from that moment that I would never let it go. I had to solve it." – Sir Andrew Wiles about his proof of Fermat's Last Theorem.
-
Carl Friedrich Gauss's Disquisitiones Arithmeticae, first edition. This book was very important for modern number theory.
-
Carl Friedrich Gauss, a German mathematician who made huge contributions to number theory.
-
Ernst Kummer, a German mathematician who worked on Fermat's Last Theorem.
-
Peter Gustav Lejeune Dirichlet, a German mathematician who made important advances in number theory.
-
Number theorists Paul Erdős and Terence Tao in 1985, when Erdős was 72 and Tao was 10. Both are famous for their work with numbers.
-
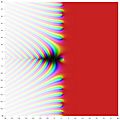
Riemann zeta function ζ(s) in the complex plane. This function is used to study the distribution of prime numbers.
See also
In Spanish: Teoría de números para niños
