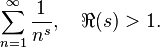Riemann zeta function facts for kids

The Riemann zeta function ζ(s) shown in the complex plane. The colors help us see the value of ζ(s): bright colors mean values close to zero, and the color's shade shows the value's direction. The white spot at s= 1 is where the function goes to infinity (a "pole"); the black spots on the left and on the critical line are where the function equals zero (its "zeros").

This image explains the colors used in the picture above. For example, numbers that are positive and real are shown in red.

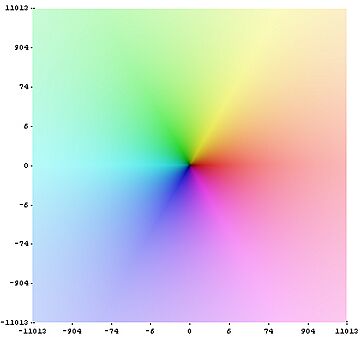
In mathematics, the Riemann zeta function is a special kind of function that is very important in number theory. It is named after a German mathematician named Bernhard Riemann. This function is key to understanding how prime numbers are spread out. It is also used in other areas like physics, probability theory, and statistics.

What is the Riemann Zeta Function?

The Riemann zeta function can be described using a mathematical sum. For certain numbers, it looks like this:

This means you add up an endless list of fractions: 1/1^s + 1/2^s + 1/3^s + and so on. The letter s here stands for a complex number. A complex number is a number that can include the square root of -1, often written as i.

However, this simple sum only works for some numbers where the real part of s is greater than 1. To make it work for almost all other numbers, Riemann used a clever mathematical trick called analytic continuation. This allowed the function to be defined for nearly every number, except for the number 1, where the function becomes infinitely large.

History of the Riemann Zeta Function

The first ideas about this function were discovered by Leonhard Euler in the 1700s. But it was named after Bernhard Riemann because of his important paper published in 1859. This paper was called "On the Number of Primes Less Than a Given Quantity".

The Riemann Hypothesis

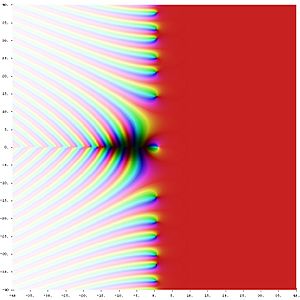
The Riemann hypothesis is a big puzzle in mathematics. It is a guess about where the Riemann zeta function equals zero. These "zeros" are special points where the function's value is exactly zero. Many mathematicians believe the Riemann hypothesis is the most important unsolved problem in pure mathematics. Finding the answer would help us understand a lot more about prime numbers.

Images for kids

• 

  This image shows the "pole" at z=1 (where the function goes to infinity) and two "zeros" on the critical line (where the function is zero).

See also

In Spanish: Función zeta de Riemann para niños