Function (mathematics) facts for kids

A function takes an input and gives an output.

In mathematics, a function is like a special rule or a machine. It takes an input and gives you exactly one output. Think of it as a vending machine: you put in money (input), and you get a specific snack (output).

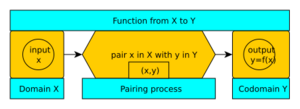
The set of all possible inputs is called the domain. The set of all possible outputs is called the codomain. Functions are often named with letters like f, g, or h.

When we say y is a function of x, we write it as 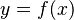. Here, f is the name of the function. We can also write 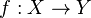to show that the function f takes inputs from set X (the domain) and produces outputs in set Y (the codomain).

For example, 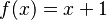is a function. If you input a natural number like 0, 1, 2, or 3, the function adds 1 to it. So, 0 becomes 1, 1 becomes 2, and so on. Functions don't always have to be simple equations. The main idea is that each input is paired with only one output.

How to Understand Functions

Functions help us understand how different things are connected. We can show functions in different ways, like using tables or graphs.

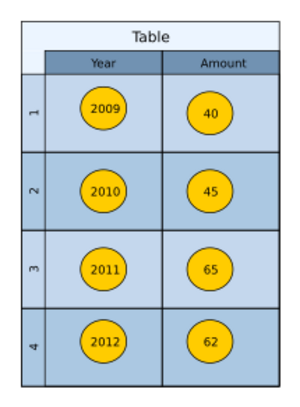
Functions in Tables

Inputs and outputs of a function can be shown in a table.

One easy way to see how a function works is to put its inputs and outputs into a table. This is helpful when you don't have too many pairs of data. Each row shows an input and its matching output.

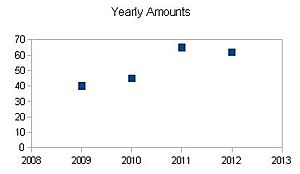
Functions on Graphs

Each input (like 1, 2, 3) must have only one output (like a, b, c, d).

When inputs and outputs have an order, we can plot them on a graph. This helps us see the relationship visually. For example, if you plot 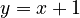Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): y=x+1 , you'll see a straight line.

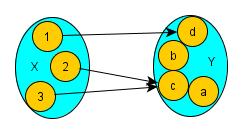
It's important that each input has only one output. Look at the picture: input 2 gives output 'c', and input 3 also gives output 'c'. This is allowed. But input 2 could not give both 'c' and 'd' at the same time. Each input must lead to just one specific output.

The set of all actual outputs that a function produces is called its image. The image is always a part of the codomain.

A graph shows the relationship between inputs and outputs.

History of Functions

The idea of a "function" has changed over time.

In the 1690s, mathematicians like Gottfried Leibniz and Johann Bernoulli started using the word "function." This was around the same time that calculus was being developed.

Later, in 1748, Leonhard Euler described a function as an "analytic expression." This meant it was a formula made of variables and numbers. In 1755, he expanded this idea, saying that if some quantities depend on others, they are functions of those others.

Peter Gustav Lejeune Dirichlet is often given credit for the first modern definition of a function in 1837. He said that for every value of x in a certain range, there must be a specific value of y. It didn't matter how this connection was made. This definition was used in schools for a long time.

In 1939, a group of mathematicians called Bourbaki made Dirichlet's definition even more general. They described a function as a connection between inputs and outputs using set theory. This version became common in schools around the 1960s.

Types of Functions

There are many different kinds of functions in mathematics:

• Elementary functions are the ones you usually learn about in school. These include things like fractions, square roots, and trigonometric functions (like sine, cosine, and tangent).
• Non-elementary functions are more complex. Many integrals are examples of non-elementary functions. They often involve operations beyond simple addition, subtraction, multiplication, and powers.
• Inverse functions are functions that "undo" another function. If a function f(x) gives you y, then its inverse function, let's call it F(y), will give you x back. Not every function has an inverse.
• Special functions are functions that have specific names because they are used a lot in math and science. Examples include sine, cosine, and tangent. A simple function like f(x)=3x (three times x) is not usually called a special function. Special functions can be elementary, non-elementary, or inverses.

Related pages

• Constant function
• Continuous function
• Function composition
• Special functions
  • Gamma function
  • Matrix function
• Linear function
• Lucy Joan Slater - A British mathematician who studied mathematical functions.
• MATLAB, Wolfram Mathematica - software programs used to work with mathematical functions.
• Relation (mathematics)

See also

In Spanish: Función (matemática) para niños