Relation (mathematics) facts for kids

A Mathematics relation shows how things in one group are connected to things in another group. Think of it like matching items from two different lists. For example, if you have a list of students and a list of their favorite colors, a relation could show which student likes which color.

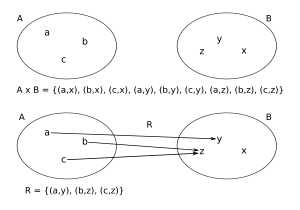
In math, a relation is a set of pairs. Each pair connects one item from the first group to one item from the second group. The most common type is a binary relation, which connects items from two groups. If the relation connects items within the same group, it's called homogeneous.

For example, a line drawn on a graph is a relation. It connects numbers on the X-axis to numbers on the Y-axis.

A relation R connects items from set A to set B. This picture shows sets A={a,b,c} and B={x,y,z}. A relation is a way to link elements between these sets. Functions are a special kind of relation.

What Are Relations?

Imagine you have two groups of things, like a group of students and a group of subjects they study. A relation could be "studies". So, you might have pairs like (Maria, Math), (Tom, Science), and (Maria, History). This shows how students and subjects are connected.

In math, these groups are called sets. A relation is simply a collection of pairs from these sets. The first item in each pair comes from the first set, and the second item comes from the second set.

Domain and Codomain

The set of all starting points in a relation is called the domain. The set of all possible ending points is called the codomain. For example, in our student-subject relation, the students would be the domain, and the subjects would be the codomain.

Relations in Databases

In computer science, especially with relational databases, relations are often called tables. Each row in a table is like one of our pairs, and each column is a type of item.

For example, a table of students might have columns for "Student Name" and "Favorite Color". Each row would be a pair, like (Sarah, Blue).

Databases use special rules to organize these tables. This helps make sure the information is clear and correct. It also prevents mistakes when adding or changing data.

Different Kinds of Relations

Relations can have different properties. These properties help us understand how the items in the sets are connected.

Functions: A Special Relation

A function is a special type of relation. In a function, each item in the first set (the domain) is connected to only one item in the second set (the codomain).

Think of a vending machine. When you press a button (an item from the first set), you get only one specific snack (an item from the second set). You don't get two different snacks from one button.

Equivalence Relations

An equivalence relation is like saying things are "equal to" each other in some way. For example, if you have a group of friends, "being the same age as" could be an equivalence relation.

Equivalence relations have three main properties:

• Reflexive: Something is always related to itself. (You are the same age as yourself.)
• Symmetric: If A is related to B, then B is related to A. (If you are the same age as your friend, your friend is the same age as you.)
• Transitive: If A is related to B, and B is related to C, then A is related to C. (If you are the same age as your friend, and your friend is the same age as another person, then you are the same age as that other person.)

Order Relations

An order relation helps us put things in order, like "smaller than" or "taller than".

For example, the "smaller than" relation:

• If X is smaller than Y, and Y is smaller than Z, then X is smaller than Z. This is a transitive property.
• If X is smaller than Y, then Y is not smaller than X. This is an asymmetric property.

Symmetric Relations

A relation is symmetric if whenever (A, B) is a pair, then (B, A) is also a pair. The "is equal to" relation is symmetric. If X is equal to Y, then Y is equal to X.

Asymmetric Relations

A relation is asymmetric if whenever (A, B) is a pair, then (B, A) is not a pair. The "is smaller than" relation is asymmetric. If X is smaller than Y, Y cannot be smaller than X.

Reflexive Relations

A relation is reflexive if every item is related to itself. The "is equal to" relation is reflexive. For any X, X is equal to X.

Images for kids

• 

  Examples of four types of binary relations over the real numbers: one-to-one (in green), one-to-many (in blue), many-to-one (in red), many-to-many (in black).