Matrix function facts for kids

A function in math takes an input and gives an output. Think of it like a machine: you put something in, and something else comes out. A matrix function is special because both its input and output are matrices. A matrix is like a grid of numbers.

Matrix functions are a cool part of linear algebra, which is a branch of mathematics that deals with vectors, vector spaces, and matrices.

What are Matrix Functions?

Imagine you have a regular math function, like one that squares a number, or adds 5 to it. A matrix function does something similar, but instead of a single number, it works with a whole grid of numbers (a matrix).

Let's say you have a simple math function, like a polynomial:

• Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): f(x) = 2 + 3x + 4x^2

If you want to use this function with a matrix, let's call it , you can do it! You would write:

• Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): f(A) = 2I + 3A + 4A^2

Here, 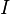stands for the identity matrix. It's a special matrix that acts like the number '1' in matrix math. When you multiply a matrix by the identity matrix, the matrix doesn't change.

So, a matrix function lets you apply common math operations, like adding, multiplying, or even more complex ones, directly to matrices.

Examples of Matrix Functions

Many common functions you know can be turned into matrix functions. For example:

• The matrix exponential (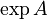Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \exp A ): This is like the regular exponential function (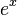) but for matrices. It's very important in solving problems about how things change over time, like in physics or engineering.
• Matrix trigonometric functions (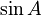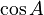Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \sin A , Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \cos A ): These are like the sine and cosine functions you learn in geometry, but they work with matrices.
• The matrix logarithm (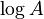Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \log A ): This is the opposite of the matrix exponential, just like a regular logarithm is the opposite of an exponential.
• The matrix square root (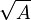Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \sqrt{A} ): This finds a matrix that, when multiplied by itself, gives you the original matrix.

Why are Matrix Functions Important?

Matrix functions are not just cool math tricks; they are very useful in the real world!

• Solving Problems: They help scientists and engineers solve complex problems in areas like differential equations. These equations describe how things change, like the path of a rocket or the flow of heat.
• Statistics: In statistics, matrix functions are used to analyze large sets of data. This helps us understand patterns and make predictions.
• Computer Science: People who work in numerical analysis (which is about how computers solve math problems) study matrix functions a lot. They want to find the fastest and most accurate ways for computers to calculate these functions. This is important for everything from creating realistic computer graphics to designing new technologies.

Matrix functions are a powerful tool that helps us understand and work with complex systems in many different fields.

Related Areas of Study

• Matrix analysis: This is the study of matrices and their functions.
• Numerical linear algebra: This field focuses on how to use computers to solve problems involving matrices.