Matrix (mathematics) Facts for Kids

Specific entries of a matrix are often referenced by using pairs of subscripts, for the numbers at each of the rows & columns.

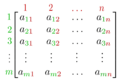
In mathematics, a matrix (say "MAY-trix", plural: matrices - say "MAY-tri-sees") is like a rectangle made of numbers. These numbers are neatly arranged in rows (horizontal lines) and columns (vertical lines). Think of it like a grid or a spreadsheet! The first number is always at the top-left, in row 1, column 1.

Matrices are usually shown with big letters like A, B, or C. There are special rules for adding, subtracting, and multiplying matrices. These rules are different from how you add or multiply regular numbers. For example, if you multiply matrix A by matrix B (written as AB), you might not get the same answer as multiplying B by A (written as BA). This is different from regular numbers where 2 x 3 is always the same as 3 x 2.

A matrix can have more than two dimensions, like a 3D matrix. It can also be one-dimensional, meaning it's just a single row or a single column of numbers.

Matrices are super important in many science fields. Many universities teach courses about matrices, often called linear algebra, very early on. You'll find matrices used a lot in computer science, engineering, physics, economics, and statistics.

What Are Matrices?
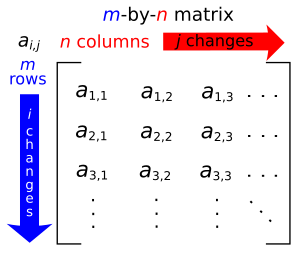
- An Example Matrix
How to Work with Matrices
- Adding Matrices
- Multiplying Matrices
Special Kinds of Matrices
Determinants
Related Pages
Images for kids
See also

What Are Matrices?

The horizontal lines in a matrix are called rows. The vertical lines are called columns. A matrix with m rows and n columns is called an m-by-n matrix (or m×n matrix). The numbers m and n tell you its dimensions.

The individual numbers inside the matrix are called entries or elements. If you want to talk about a specific number in a matrix A, you'd say it's the i,j entry. This means it's in row i and column j. We write this as A[i,j] or a_i,j.

An Example Matrix

Let's look at an example: 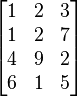$\begin{bmatrix} 1 & 2 & 3 \\ 1 & 2 & 7 \\ 4 & 9 & 2 \\ 6 & 1 & 5 \end{bmatrix}$

This matrix has 4 rows and 3 columns. So, it's a 4×3 matrix. Here, m=4 and n=3.

Can you find the entry A[2,3] (or a_2,3)? It's the number in the 2nd row and 3rd column. In this example, a_2,3 is 7.

How to Work with Matrices

You can do different math operations with matrices, like adding and multiplying them.

Adding Matrices

Adding two matrices is pretty straightforward! You just add the numbers in the same positions. For example, the number in row 1, column 1 of the first matrix is added to the number in row 1, column 1 of the second matrix.

Here's an example: 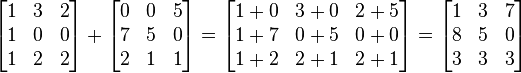$\begin{bmatrix} 1 & 3 & 2 \\ 1 & 0 & 0 \\ 1 & 2 & 2 \end{bmatrix} + \begin{bmatrix} 0 & 0 & 5 \\ 7 & 5 & 0 \\ 2 & 1 & 1 \end{bmatrix} = \begin{bmatrix} 1+0 & 3+0 & 2+5 \\ 1+7 & 0+5 & 0+0 \\ 1+2 & 2+1 & 2+1 \end{bmatrix} = \begin{bmatrix} 1 & 3 & 7 \\ 8 & 5 & 0 \\ 3 & 3 & 3 \end{bmatrix}$

Important: You can only add two matrices if they have the exact same dimensions (the same number of rows and columns). When you add matrices, the order doesn't matter. So, A + B is always the same as B + A.

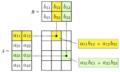
Multiplying Matrices

Multiplying matrices is a bit trickier than adding them. You don't just multiply the numbers in the same spots. Instead, you multiply rows by columns.

Here's how it works for two 2x2 matrices: 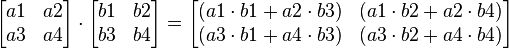$\begin{bmatrix} a1 & a2 \\ a3 & a4 \\ \end{bmatrix} \cdot \begin{bmatrix} b1 & b2 \\ b3 & b4 \\ \end{bmatrix} = \begin{bmatrix} (a1\cdot b1 + a2 \cdot b3) & (a1 \cdot b2 + a2 \cdot b4) \\ (a3\cdot b1 + a4 \cdot b3) & (a3 \cdot b2 + a4 \cdot b4) \\ \end{bmatrix}$ Let's try it with numbers: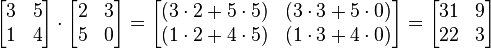 $\begin{bmatrix} 3 & 5 \\ 1 & 4 \\ \end{bmatrix} \cdot \begin{bmatrix} 2 & 3 \\ 5 & 0 \\ \end{bmatrix} = \begin{bmatrix} (3\cdot 2 + 5 \cdot 5) & (3 \cdot 3 + 5 \cdot 0) \\ (1\cdot 2 + 4 \cdot 5) & (1 \cdot 3 + 4 \cdot 0) \\ \end{bmatrix} = \begin{bmatrix} 31 & 9 \\ 22 & 3 \\ \end{bmatrix}$

You can only multiply two matrices if the number of columns in the first matrix is the same as the number of rows in the second matrix.
The new matrix you get (the "product") will have the same number of rows as the first matrix and the same number of columns as the second matrix.
Remember, the order usually matters! 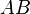Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): AB is generally NOT the same as $BA$ .
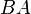However, if you have three matrices, (AB)C is the same as A(BC). This is called the associative property.

Special Kinds of Matrices

Some matrices have unique properties that make them special.

Square Matrix

A square matrix is a matrix that has the same number of rows as columns. So, if it has m rows, it also has m columns.

Here's an example of a square matrix: 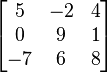$\begin{bmatrix} 5 & -2 & 4 \\ 0 & 9 & 1 \\ -7 & 6 & 8 \\ \end{bmatrix}$

This matrix has 3 rows and 3 columns, so it's a 3x3 square matrix.

Identity Matrix

For every size of square matrix, there's a special matrix called the identity matrix. It's usually shown with the symbol 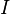$I$ . The identity matrix has ones along its main diagonal (from top-left to bottom-right) and zeroes everywhere else.

For example, a 3x3 identity matrix looks like this: 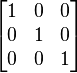$\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{bmatrix}$ There's only one identity matrix for each size (like 2x2, 3x3, etc.). What makes it special is that when you multiply any matrix by the identity matrix, the original matrix stays exactly the same! It's like multiplying a regular number by 1.

Inverse Matrix

An inverse matrix is like the "opposite" of another matrix. When you multiply a matrix by its inverse, the result is the identity matrix.

For example: $\begin{bmatrix} 7 & 8 \\ 6 & 7 \\ \end{bmatrix} \cdot \begin{bmatrix} 7 & -8 \\ -6 & 7\\ \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ \end{bmatrix}$ Here, Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \begin{bmatrix} 7 & -8 \\ -6 & 7 \\ \end{bmatrix} is the inverse of Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \begin{bmatrix} 7 & 8 \\ 6 & 7 \\ \end{bmatrix} . Not all matrices have an inverse.

Column Matrix

A matrix that has many rows but only one column is called a column vector. It's just a list of numbers stacked vertically.

Determinants

For a square matrix, you can calculate a single number called its determinant. This number tells you something important about the matrix. Imagine each column of the matrix as a vector (an arrow with a direction and length). For a 2x2 matrix, the determinant tells you the area of the parallelogram formed by these two vectors.

For a 2x2 matrix like this: Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \begin{bmatrix} a & b \\ c & d \\ \end{bmatrix} The formula for its determinant is simple: $\det\left( \begin{bmatrix} a & b \\ c & d \\ \end{bmatrix}\right) =ad - bc$

For bigger matrices, like 3x3 or larger, the formula for the determinant gets much more complicated. Computers are often used to calculate determinants for large matrices.

Images for kids

An $m \times n$ matrix: the $m$ rows are horizontal and the $n$ columns are vertical. Each element of a matrix is often denoted by a variable with two subscripts. For example, $a 2,1$ represents the element at the second row and first column of the matrix.
Schematic depiction of the matrix product AB of two matrices A and B.

Matrix (mathematics) facts for kids

Contents