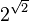Number facts for kids

For the book in the Bible, see Numbers (Bible)

A Sudoku puzzle uses numbers.

A number is a basic idea in mathematics. We use numbers to count things or to measure them. For example, you might count how many friends you have, or measure how tall you are.

Numbers help us understand the world around us. Mathematics uses numbers to explore how things work and to create new inventions. When we use numbers to study the natural world, it's called science. When we use numbers to design and build things, it's called engineering.

There are different ways to think about numbers:

Cardinal numbers tell us "how many." For example, if you have three apples, the number "3" is a cardinal number.
Ordinal numbers tell us the order of things. For example, "first," "second," or "third" are ordinal numbers.

How We Write Numbers
- Numbers for People
- Numbers for Machines
Names of Numbers
Different Kinds of Numbers
See also

How We Write Numbers

Numbers for People

Khmer Numerals - 605 from the Sambor inscriptions

The number 605 in Khmer numerals from 683 AD. This shows an early use of zero.

People use different ways to write down numbers. These systems are called number systems. The most common system we use every day is the base ten number system. It's also known as the decimal number system.

This system is popular because most people have ten fingers and ten toes. It uses ten different symbols, called digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9.

The position of each digit in a number shows its value. For example, the number 23 means (2 times 10) plus 3. The number 101 means (1 times 100) plus (0 times 10) plus (1 times 1).

Numbers for Machines

Another number system is very important for machines, like computers. This is called the binary number system, or the base two system. It uses only two symbols: 0 and 1. These symbols are called bits.

Just like in the decimal system, the position of the bits shows the number's value. For example, the binary number 10 means (1 times 2) plus 0. This is the same as the decimal number 2. The binary number 101 means (1 times 4) plus (0 times 2) plus (1 times 1). This is the same as the decimal number 5.

Names of Numbers

In English, we have special names for some numbers. Especially for numbers that are "powers of ten." These numbers are written with a "1" followed by one or more "0"s.

Here are some examples:

1 – one
10 – ten
100 – one hundred
1000 – one thousand
1,000,000 – one million

For very large numbers, there are two main ways to name them in English:

The short scale gives a new name every time a number is a thousand times larger. This is common in most English-speaking countries today.
The long scale gives a new name every time a number is a million times larger. This scale is less common in English-speaking countries now.

Here are some examples of large numbers:

1,000,000,000 – one billion (short scale), one milliard (long scale)
1,000,000,000,000 – one trillion (short scale), one billion (long scale)
1,000,000,000,000,000 – one quadrillion (short scale), one billiard (long scale)

Different Kinds of Numbers

Natural Numbers

Natural numbers are the numbers we use for simple counting: 1, 2, 3, 4, 5, and so on. Some people also include 0 as a natural number.

These numbers are sometimes called positive numbers. However, not all positive numbers are natural. For example, 1/2 is positive but not a natural number. To avoid confusion, it's often clearer to say "positive integers" or "non-negative integers."

Negative Numbers

Negative numbers are numbers that are less than zero.

Imagine a number line. We mark one spot as zero. Numbers to the right of zero are positive. Numbers to the left of zero are negative. For example, if 1 is one step to the right, then minus 1 (−1) is one step to the left.

A number line showing positive and negative integers.

You can do math with negative numbers:

Adding a negative number is like subtracting a positive one. For example, 5 + (−3) is the same as 5 − 3, which equals 2.
Subtracting a negative number is like adding a positive one. For example, 5 − (−3) is the same as 5 + 3, which equals 8.
Multiplying two negative numbers gives a positive number. For example, −5 times −3 equals 15.
Multiplying a negative number by a positive number (or vice versa) gives a negative number. For example, 5 times −3 equals −15.

Integers

Integers include all the natural numbers, their opposites (the negative numbers), and zero. Integers are whole numbers. They do not include decimal numbers or fractions. So, -3, 0, and 5 are integers, but 2.5 or 1/2 are not.

Rational Numbers

Rational numbers are numbers that can be written as fractions. This means you can write them as a divided by b, where a and b are integers, and b is not zero.

Some rational numbers, like 1/10, have a finite number of digits after the decimal point. For example, 1/10 is 0.1. Other rational numbers, like 1/11, have an infinite number of digits that repeat in a pattern. For example, 1/11 is 0.090909...

A percentage is also a rational number. For example, 7% can be written as the fraction 7/100 or the decimal 0.07.

Irrational Numbers

Irrational numbers are numbers that cannot be written as a simple fraction. They also don't have an imaginary part (which we'll explain next).

The square root of 2 (√2) is an irrational number.

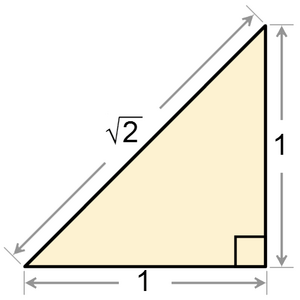
Irrational numbers often appear in geometry. For example, if you have a square with sides of 1 meter, the distance across its opposite corners is the square root of two (√2). This number is about 1.414213... It goes on forever without repeating. Mathematicians have proven that the square root of any natural number is either a whole number or an irrational number.

A famous irrational number is pi (π). Pi is the circumference (distance around) of any circle divided by its diameter (distance across). Pi is approximately 3.1415926535... Its digits go on forever without repeating.

Real Numbers

Real numbers include all the types of numbers we've talked about so far:

The rational numbers (like integers and fractions)
The irrational numbers (like pi and square roots of non-perfect squares)

Basically, real numbers are all the numbers that don't involve imaginary numbers. You can place any real number on a number line.

Imaginary Numbers

Imaginary numbers are formed by multiplying a real number by the special number i. This number i is defined as the square root of minus one (−1).

In the world of real numbers, you can't find a number that, when multiplied by itself, equals −1. So, mathematicians created this new number, i, calling it the imaginary unit.

Imaginary numbers follow similar math rules:

To add two imaginary numbers, you add their real parts and keep the i. For example, 2i + 3i = (2 + 3)i = 5i.
To subtract two imaginary numbers, you subtract their real parts. For example, 5i − 3i = (5 − 3)i = 2i.
When multiplying two imaginary numbers, remember that i × i (which is i²) equals −1. For example, 5i × 3i = (5 × 3) × (i × i) = 15 × (−1) = −15.

They were called "imaginary" because when they were first discovered, many mathematicians thought they weren't "real" numbers.

Complex Numbers

Complex numbers are numbers that have two parts: a real part and an imaginary part. Every type of number we've discussed so far is also a complex number. For example, 5 is a complex number (with an imaginary part of 0i), and 3i is a complex number (with a real part of 0).

Complex numbers are a more general way to describe numbers. You can show them on a special graph called a complex plane. This plane has a real number line (horizontal) and an imaginary number line (vertical).

3i|_ | | 2i|_ . 2+2i | | i|_ | | |_____|_____|_____|_____|_____|_____|_____|_____| −2 −1 0 1 2 3 4 5 6 | −i|_ .3−i | | .−2−2i −2i|_ | | −3i|_ |

You can do all normal math operations with complex numbers:

To add two complex numbers, you add their real parts together and their imaginary parts together. For example, (2 + 3i) + (3 + 2i) = (2 + 3) + (3 + 2)i = 5 + 5i.
To subtract one complex number from another, you subtract their real parts and their imaginary parts separately. For example, (7 + 5i) − (3 + 3i) = (7 − 3) + (5 − 3)i = 4 + 2i.

Multiplying complex numbers is a bit more involved. If you have two complex numbers, like (a + bi) and (c + di), you multiply them like this: 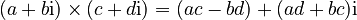Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): ( a + b \mathrm{i} ) \times ( c + d\mathrm{i} ) = ( ac - bd ) + ( ad + bc )\mathrm{i} For example, (4 + 5i) × (3 + 2i) = (4 × 3 − 5 × 2) + (4 × 2 + 5 × 3)i = (12 − 10) + (8 + 15)i = 2 + 23i.

Transcendental Numbers

A transcendental number is a real or complex number that cannot be the solution to a simple algebraic equation. An algebraic equation looks like this: 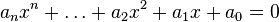$a_{n}x^{n} + \dots + a_{2}x^2 + a_{1}x + a_{0} = 0$ Here, the 'a' values are integers (whole numbers).

It can be very hard to prove that a number is transcendental. Every transcendental number is also an irrational number. The first mathematicians to think about transcendental numbers were Gottfried Wilhelm Leibniz and Leonhard Euler. The first person to actually prove that such numbers exist was Joseph Liouville in 1844.

Some well-known transcendental numbers include:

e (Euler's number)
π (pi)
e^a for any algebraic number 'a' that is not zero
$2^{\sqrt{2}}$