Binary number Facts for Kids

The binary numeral system is a special way to write numbers. Instead of using ten different digits like we normally do (0, 1, 2, 3, 4, 5, 6, 7, 8, 9), binary only uses two: 0 and 1.

Think of it like a light switch. A 0 means "off," and a 1 means "on." This is why binary is super important for computers! Computers use these "off" and "on" signals to understand and process information.

In our normal number system (called decimal), each digit's place value is 10 times bigger than the one to its right (like ones, tens, hundreds, thousands). But in binary, each digit's place value is twice as much as the one to its right. The digit on the far right always has a value of 1.

Let's look at an example of a binary number: 10110011. We can figure out what this means in our normal numbers:

The last 1 (on the far right) means 1.
The 1 before that means 2.
The 0 before that means 4.
The 0 before that means 8.
The 1 before that means 16.
The 1 before that means 32.
The 0 before that means 64.
The 1 before that means 128.

To find the total value, we add up all the place values where there is a 1. So, 1 + 2 + 16 + 32 + 128 = 179. So, 10110011 in binary is 179 in our normal numbers!

0	0000	0+0+0+0
1	0001	0+0+0+1
2	0010	0+0+2+0
3	0011	0+0+2+1
4	00100	0+0+4+0+0
5	00101	0+0+4+0+1
6	00110	0+0+4+2+0
7	00111	0+0+4+2+1
8	01000	0+8+0+0+0
9	01001	0+8+0+0+1
10	01010	0+8+0+2+0
11	01011	0+8+0+2+1
12	01100	0+8+4+0+0
13	01101	0+8+4+0+1
14	01110	0+8+4+2+0
15	01111	0+8+4+2+1
16	10000	16+0+0+0+0
17	10001	16+0+0+0+1
18	10010	16+0+0+2+0
19	10011	16+0+0+2+1
20	10100	16+0+4+0+0
21	10101	16+0+4+0+1
22	10110	16+0+4+2+0
23	10111	16+0+4+2+1
24	11000	16+8+0+0+0
25	11001	16+8+0+0+1
26	11010	16+8+0+2+0
27	11011	16+8+0+2+1
28	11100	16+8+4+0+0
29	11101	16+8+4+0+1
30	11110	16+8+4+2+0
31	11111	16+8+4+2+1

For convenience, binary digits are often grouped. Each binary digit (a 0 or a 1) is called a bit. When you have 8 bits together, it's called a byte. You might hear these terms when talking about computer memory!

Binary Math
History of Binary
How to Translate Binary
Related pages
Images for kids
See also

Binary Math

Just like with regular numbers, you can do math with binary numbers. Here are the basic rules for adding them:

0 + 0 = 0
1 + 0 = 1
1 + 1 = 10 (This is like saying 1 + 1 = 2 in binary. Since there's no digit '2', you carry over, just like when 5 + 5 = 10 in decimal.)
1 + 1 + 1 = 11 (This is like saying 1 + 1 + 1 = 3 in binary.)

Let's see why 1 + 1 + 1 equals 11 in binary:

Column	Decimal Value	Binary
1 (left column)	2	1
2 (right column)	1	1

When you add 1 + 1 + 1, you get 3. In binary, 3 is written as 11. The rightmost '1' means 1, and the leftmost '1' means 2. So, 1 + 2 = 3.

History of Binary

The binary numeral system, in a manuscript by Gottfried Wilhelm Leibniz, 1697

A page from Explication de l’Arithmétique Binaire, by Leibniz, 1703

Many people have explored numbering systems using only two symbols. However, the modern binary number system we use today is mostly credited to Gottfried Leibniz. He was a German mathematician who wrote about it in 1679.

Binary is used in almost every electronic device. From simple calculators to powerful supercomputers, binary is the language they speak! The special code that computers understand, called Machine code, is made up of binary digits.

How to Translate Binary

You can translate binary numbers into our normal decimal numbers using powers of 2.

For example, let's translate 10110: 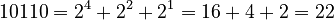Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 10110 = 2^4 + 2^2 + 2^1 = 16 + 4 + 2 = 22 Here's how it works: