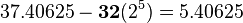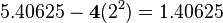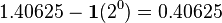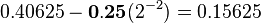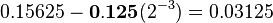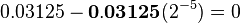Floating point facts for kids
Computers store numbers in a special way. They usually work with binary whole numbers. But what about numbers with decimals, like 3.14? Computers can't directly store these. To solve this, they use something called floating-point representation. The "floating" part means the decimal point can move. It can shift left or right, like when you multiply a number by a power of ten. This helps computers handle very large or very small numbers.
Contents
How Computers Store Numbers
In mathematics and science, people often use scientific notation. This makes very large or very small numbers easier to read. For example, it's easier to write 1.2 trillion as 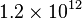 . This is much simpler than writing 1,200,000,000,000. You can also use negative powers of ten for small numbers. For instance, 0.000001 can be written as
. This is much simpler than writing 1,200,000,000,000. You can also use negative powers of ten for small numbers. For instance, 0.000001 can be written as 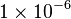 .
.
Computers use a similar idea for numbers with decimals. They use three parts to represent a number in binary:
- The sign bit: This is a single binary digit (0 or 1). It tells if the number is positive (0) or negative (1).
- The significand: This is like the main part of the number. It's a whole number version of the original number.
- The exponent: This is the power you multiply the base by. It tells you how many places the decimal point moved.
What is the Significand?
The significand is found by moving the decimal point in your number. You move it until there are no decimal parts left. This turns your number into a whole number. For example, in decimal, 1.45 becomes 145 by moving the point two steps to the right.
In binary, if you have 1101.0111 (which is 13.4375 in decimal), you move the binary point four steps right. This makes it 11010111 (which is 215 in decimal). The goal is to make the number a whole number. This way, computers can store it easily in bytes and use it in calculations.
What is the Exponent?
The exponent tells you how many places the decimal point moved. If the point moved left, the exponent is negative. If it moved right, the exponent is positive.
Let's look at our example: turning 1.45 into 145. You moved the point two places right. This means you multiplied by 100. Since 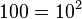 , the exponent is 2.
, the exponent is 2.
For binary, turning 1101.0111 (13.4375) into 11010111 (215) means moving the binary point four places to the right. So, the exponent is 4.
Computers often use a "biased" exponent. This means they add a fixed number (like 127 for 32-bit numbers) to the actual exponent. This avoids needing a separate sign bit for the exponent itself.
- If the exponent is 5, the biased exponent is
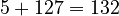 . In binary, this is 1000 0100.
. In binary, this is 1000 0100. - If the exponent is -5, the biased exponent is
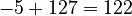 . In binary, this is 0111 1010.
. In binary, this is 0111 1010. - If the exponent is 0, the biased exponent is
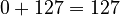 . In binary, this is 0111 1111.
. In binary, this is 0111 1111.
Example: Decimal to Floating-Point Binary
Let's see how to represent the decimal number 37.40625 in binary. This is sometimes called a "bicimal" or "binary decimal."
First, we convert 37.40625 from base 10 (decimal) to base 2 (binary). We do this by finding the largest powers of two that fit into the number and subtracting them.
Using these powers of two, we can write 37.40625 in binary:
| Power: | 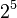 |
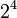 |
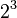 |
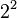 |
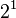 |
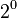 |
• | 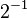 |
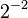 |
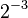 |
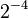 |
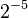 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Value: | 1 | 0 | 0 | 1 | 0 | 1 | • | 0 | 1 | 1 | 0 | 1 |
So, 37.40625 in binary is 100101.01101.
Converting Binary to Float
Now we have our binary number: 100101.01101. Computers need to store this as a floating-point number. A common way is using the IEEE-754 standard for 32-bit floating-point numbers. This number has three parts:
- Sign (1 bit): 0 for positive, 1 for negative. Our number 37.40625 is positive, so the sign bit is 0.
- Exponent (8 bits): This tells us how many places the binary point moved. We need to move the binary point in 100101.01101 to make it a whole number. We move it 5 places to the right to get 10010101101. So, our exponent is 5. For a 32-bit float, we add 127 to the exponent (5 + 127 = 132).
- Significand (23 bits): This is our binary number without the binary point. For 100101.01101, the significand is 10010101101. We fill the remaining bits with zeros to make it 23 bits long.
Here's how 37.40625 looks as a 32-bit floating-point number:
| Type: | ± |
Exponent | Significand | |||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Value: | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| Meaning: | + | 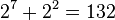 |
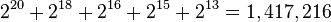 |
|||||||||||||||||||||||||||||
Related pages
Images for kids
-
Single-precision floating point numbers on a number line: the green lines mark representable values.
-
Augmented version above showing both signs of representable values
-
Leonardo Torres y Quevedo, who proposed a form of floating point in 1914
-
Konrad Zuse, architect of the Z3 computer, which uses a 22-bit binary floating-point representation
-
William Kahan. A primary architect of the Intel 80x87 floating-point coprocessor and IEEE 754 floating-point standard.
See also
 In Spanish: Coma flotante para niños
In Spanish: Coma flotante para niños