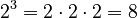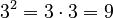Exponentiation facts for kids
Exponentiation is a special math operation that helps us multiply a number by itself many times. Think of it like a super-fast way to do repeated multiplication, just as multiplication is a fast way to do repeated addition!
When you see a number like 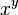 , it means you multiply the number
, it means you multiply the number  by itself
by itself  times. We read this as "
times. We read this as " raised to the power of
raised to the power of  " or "
" or " to the
to the  th power."
th power."
In 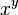 :
:
- The number
 is called the base. It's the number being multiplied.
is called the base. It's the number being multiplied. - The number
 is called the exponent (or power). It tells you how many times to multiply the base by itself.
is called the exponent (or power). It tells you how many times to multiply the base by itself.
For example, in 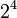 , the base is 2 and the exponent is 4. To figure out
, the base is 2 and the exponent is 4. To figure out 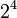 , you multiply 2 by itself 4 times:
, you multiply 2 by itself 4 times: 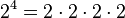 And the answer is
And the answer is 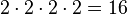 . So, "2 raised to the power of 4 equals 16."
. So, "2 raised to the power of 4 equals 16."
Here are some more examples:
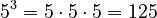
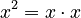
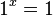 (This means 1 multiplied by itself any number of times is always 1!)
(This means 1 multiplied by itself any number of times is always 1!)
Contents
Special Exponents
Some exponents have special names or meanings.
The Square (Exponent 2)
If the exponent is 2, we call it a square. For example, 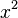 is the square of
is the square of  . This name comes from geometry! The area of a square shape is found by multiplying its side length by itself. So, if a square has a side length of a, its area is
. This name comes from geometry! The area of a square shape is found by multiplying its side length by itself. So, if a square has a side length of a, its area is 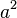 .
.
The Cube (Exponent 3)
If the exponent is 3, we call it a cube. For example, 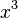 is the cube of
is the cube of  . This also comes from geometry! The volume of a cube shape is found by multiplying its side length by itself three times. So, if a cube has a side length of a, its volume is
. This also comes from geometry! The volume of a cube shape is found by multiplying its side length by itself three times. So, if a cube has a side length of a, its volume is 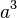 .
.
Negative Exponents
When the exponent is a negative number, it means you take the reciprocal of the base. The reciprocal of a number is 1 divided by that number.
- If the exponent is -1, it's simply the reciprocal:
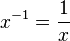
- If the exponent is any negative integer (whole number), you take the reciprocal and then raise it to the positive version of that exponent:
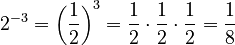
Fractional Exponents (Roots)
Sometimes, the exponent can be a fraction!
- If the exponent is
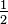 , it means you find the square root of the base:
, it means you find the square root of the base:
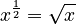 For example:
For example: 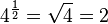 (because
(because 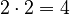 ).
).
- If the exponent is
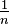 , it means you find the nth root:
, it means you find the nth root:
![a^{\frac{1}{n}} = \sqrt[n]{a}](/images/math/c/d/e/cde604330dc8b9bb773376cb1fbf2098.png)
- If the exponent is a rational number (a fraction) like
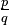 , it means you take the qth root of the base, and then raise that result to the power of p:
, it means you take the qth root of the base, and then raise that result to the power of p:
![a^{\frac{p}{q}} = \sqrt[q]{a^p}](/images/math/d/1/6/d16207859e88dd632865a3019610698c.png)
Rules of Exponents
There are some helpful rules that make working with exponents easier:
- Multiplying bases with the same exponent:
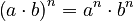 Example:
Example:  . Also,
. Also, 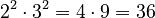 .
.
- Dividing bases with the same exponent:
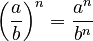 (as long as
(as long as 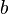 is not 0) Example:
is not 0) Example: 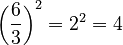 . Also,
. Also, 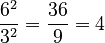 .
.
- Multiplying powers with the same base: Add the exponents.
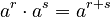 Example:
Example: 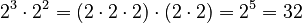 . Using the rule:
. Using the rule: 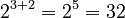 .
.
- Dividing powers with the same base: Subtract the exponents.
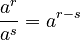 (as long as
(as long as 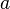 is not 0) Example:
is not 0) Example: 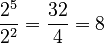 . Using the rule:
. Using the rule: 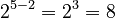 .
.
- Negative exponent rule:
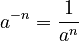 (as long as
(as long as 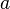 is not 0) Example:
is not 0) Example: 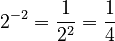 .
.
- Power of a power: Multiply the exponents.
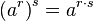 Example:
Example: 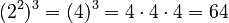 . Using the rule:
. Using the rule: 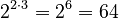 .
.
- Zero exponent: Any non-zero number raised to the power of 0 is 1.
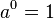 Example:
Example: 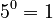 .
.
Commutativity
In math, an operation is "commutative" if the order of the numbers doesn't change the answer.
- Addition is commutative:
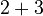 is the same as
is the same as 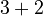 (both are 5).
(both are 5). - Multiplication is commutative:
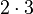 is the same as
is the same as 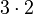 (both are 6).
(both are 6).
But exponentiation is not commutative! The order of the base and exponent matters a lot. For example:
As you can see, 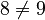 , so
, so 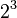 is not the same as
is not the same as 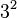 .
.
Inverse Operations
Just like addition has subtraction as its opposite (inverse) operation, and multiplication has division, exponentiation also has inverse operations. But because exponentiation is not commutative, it actually has two different inverse operations!
Let's look at examples:
- If you have
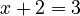 , you use subtraction to find
, you use subtraction to find 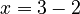 , so
, so 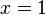 .
.
If you have 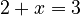 , you still use subtraction to find
, you still use subtraction to find 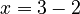 , so
, so 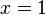 . (This works because addition is commutative).
. (This works because addition is commutative).
- If you have
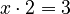 , you use division to find
, you use division to find 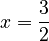 .
.
If you have 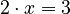 , you still use division to find
, you still use division to find 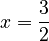 . (This works because multiplication is commutative).
. (This works because multiplication is commutative).
- Now for exponentiation:
* If you have 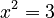 (you're looking for the base), you use the root operation to find
(you're looking for the base), you use the root operation to find  . You get
. You get 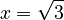 . * However, if you have
. * However, if you have 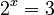 (you're looking for the exponent), you cannot use a root. Instead, you use an operation called the logarithm. You would write this as
(you're looking for the exponent), you cannot use a root. Instead, you use an operation called the logarithm. You would write this as 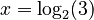 . The logarithm tells you "what power do I need to raise the base (2) to, to get the number (3)?"
. The logarithm tells you "what power do I need to raise the base (2) to, to get the number (3)?"
Related pages
See also
 In Spanish: Potenciación para niños
In Spanish: Potenciación para niños