Exponential function facts for kids
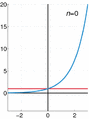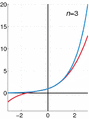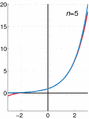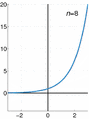
In mathematics, an exponential function is a special kind of function that grows really fast. Imagine something that doubles every minute – that's exponential growth! It's written as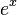 
, where 'e' is a special number called Euler's constant. This number is about 2.71828.
Contents
What Makes Them Special?
Exponential functions follow the same rules as other exponents. For example, when you multiply two exponential terms with the same base, you add their powers.
- Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): e^{x+y} = e^x e^y
This is like saying 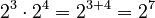Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 2^3 \cdot 2^4 = 2^{3+4} = 2^7 .
The natural logarithm is the opposite of an exponential function. It helps you find the power you need to raise 'e' to, to get a certain number.
Real-Life Examples
Exponential functions are super useful! They help us understand things that grow or shrink very quickly.
Growing Fast: Exponential Growth
You can see exponential growth in many places, like:
- Population growth: How many people live in a city over time.
- Spread of information: How quickly a video goes viral online.
- Money in a bank: This is a great example!
Let's say you put £100 in a bank account that gives you 3% interest every month. This means the bank adds 3% of your money to your account each month. The cool part is, you earn interest on the interest you've already earned!
Here's how your money would grow:
| Month | Balance | Month | Balance |
|---|---|---|---|
| January | £100.00 | July | £119.41 |
| February | £103.00 | August | £122.99 |
| March | £106.09 | September | £126.68 |
| April | £109.27 | October | £130.48 |
| May | £112.55 | November | £134.39 |
| June | £115.93 | December | £138.42 |
Notice how the amount of extra money you get each month keeps increasing. The more money you have, the more interest you earn!
Shrinking Fast: Exponential Decay
Exponential functions can also show things getting smaller very quickly. This is called exponential decay.
- Radioactive decay: How quickly radioactive materials lose their power.
- Light absorption: How light gets weaker as it passes through something.
Other Examples
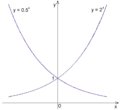
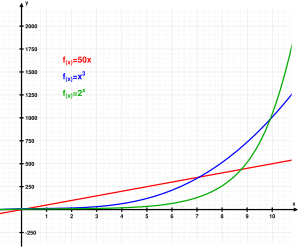
Here are some simple examples of exponential functions with different starting numbers (called the 'base'):
|
Base = 2
|
Base = 3
|
The Special Number e
Even though the base of an exponential function can be any number bigger than zero (like 2 or 10), it's often a very special number called e. This number e is approximately 2.71828. It's an irrational number, which means its decimal goes on forever without repeating.
Why is e so special? Let's go back to the bank example. Imagine a bank pays you interest very, very often, but in tiny amounts each time. If you put money in and let the interest add to your balance, your money will grow by a factor very close to e. The more often the interest is added, the closer the growth factor gets to e. This makes e super important in many areas of science and finance.
Related pages
Images for kids
-
Exponential functions with bases 2 and 1/2.
-
The blue line is the exponential function. The red lines show how we can build it up using simpler math.
-
The red curve is the exponential function. See how it climbs quickly!
See also
In Spanish: Función exponencial para niños
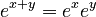
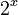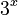