Irrational number facts for kids
An irrational number is a special kind of real number in mathematics. It's a number that you cannot write as a simple fraction (or ratio) using two integers. An integer is a whole number like 1, 2, 3, or -1, -2, -3.
Imagine trying to write an irrational number in decimal form. It would have an endless number of digits after the decimal point. Plus, these digits would never repeat in a pattern. This is what makes them different from rational numbers, which either stop or repeat their decimal digits.
Where Do We Find Irrational Numbers?
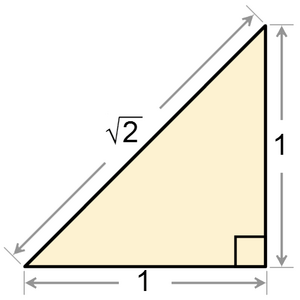
Irrational numbers pop up often in geometry. For example, imagine a square with sides that are exactly 1 meter long. If you measure the distance from one corner to the opposite corner (the diagonal), that length is the square root of two meters. This number, 1.414213..., is an irrational number.
Mathematicians have shown that the square root of any natural number (like 1, 2, 3, and so on) is either a whole number or an irrational number. For instance, the square root of 4 is 2 (a whole number), but the square root of 3 (about 1.73205...) is irrational.
Famous Irrational Numbers
One of the most famous irrational numbers is pi (π). You might have heard of it in school! Pi is found by taking the circumference (the distance around) of any circle and dividing it by its diameter (the distance across the circle through its center). No matter how big or small the circle is, this number is always the same.
Pi is approximately 3.14159265358979323... and its decimal digits go on forever without repeating.
Another important irrational number is called e. It's often used in science and finance. The number e is approximately 2.71828... and also has endless, non-repeating decimal digits.
Related pages
See also
In Spanish: Número irracional para niños
