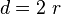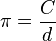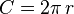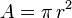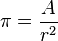Circle Facts for Kids

A circle

A circle is a perfectly round, flat shape. Imagine drawing a shape where every single point on its edge is exactly the same distance from the center. That's a circle!

The center of a circle is the point right in the middle. We often call it 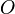$O$ .

The radius of a circle is a straight line that goes from the center to any point on the edge. Think of it like the spoke of a bicycle wheel. We use the letter r to stand for the length of the radius.

The diameter is a straight line that goes all the way across the circle, passing right through the center. It connects two points on opposite sides of the circle. We use the letter d for its length. The diameter is always twice as long as the radius:

Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): d = 2\ r

The circumference is the distance all the way around the edge of the circle. It's like the perimeter of a square or triangle, but for a circle. We use the letter C for its length.

The number π (pronounced "pie") is a very special number in math. It's a bit like a secret code that connects a circle's circumference and its diameter. If you divide the circumference of any circle by its diameter, you will always get the number pi.

\pi = \frac{C}{d}

Pi is an endless number, but we often use about 3.14159, or sometimes the fraction 22⁄7.

Because of this special relationship, we can also find the circumference if we know the radius:

C = 2\pi \, r

The area of the circle is equal to π times the area of the gray square.

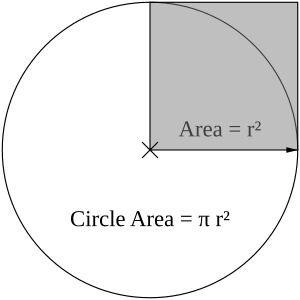
The area inside a circle, shown by the letter A, is the amount of flat space it covers. You can find the area by multiplying pi (π) by the radius, and then multiplying by the radius again (which is the same as the radius squared, or 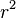$r^2$ ):

A = \pi \, r^2

Understanding Pi
- How to Find Pi
Related pages
Images for kids
See also

Understanding Pi

Pi (π) is a fascinating number that helps us understand circles. It's always the same, no matter how big or small the circle is!

How to Find Pi

You can get a good idea of what pi is by doing a simple experiment.

First, draw a large, perfect circle.
Then, carefully measure its circumference (the distance around the edge).
Next, measure its diameter (the distance straight across through the center).
Finally, divide the circumference by the diameter. You should get a number very close to 3.14!

Mathematicians have also found ways to calculate pi using only math, without needing to draw or measure anything. These methods often involve very long lists of numbers that get closer and closer to the true value of pi.

One way to think about pi is by imagining a circle drawn on a grid. If you know the radius of the circle, you can estimate its area by counting the grid squares inside it. Since the area of a circle is 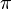$\pi$ times the radius squared ( 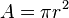$A = \pi r^2$ ), you can then find pi by dividing the estimated area by the radius squared: