Squaring the circle facts for kids
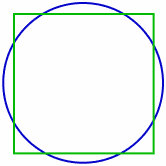
Squaring the circle is a famous challenge in geometry. It asks if you can draw a square that has the exact same area as a circle. You can only use two tools: a compass and a straightedge.
This problem is not about making a circle look like a square. It is similar to "squaring a triangle," which means finding a square with the same area as a triangle. Squaring a triangle is easy to do. However, squaring the circle is much harder.
It is one of several very old math problems that people tried to solve for a long time. Other similar problems include doubling the cube and trisecting the angle. All these problems have been proven to be impossible using only a compass and straightedge.
In 1882, a mathematician named Ferdinand von Lindenmann proved that squaring the circle is impossible. He showed this because the number π (pi) is a transcendental number. This means you cannot find its exact value using simple math operations like addition, subtraction, multiplication, division, or roots. Because you cannot find the exact value of π, you cannot find the exact side length of a square that would have the same area as a circle.
Contents
What is Squaring the Circle?
Squaring the circle means trying to build a square with the same area as a given circle. You are only allowed to use a compass and a straightedge. A compass helps you draw circles and measure distances. A straightedge helps you draw straight lines. You cannot use a ruler to measure specific lengths.
For example, if a circle has a radius of 1 unit, its area is π (pi). To "square" this circle, you would need to build a square with an area of π. This means the side length of the square would have to be the square root of π.
Why is it Impossible?
The reason squaring the circle is impossible comes down to the number π.
- Pi is a special number that helps us calculate the area and circumference of circles.
- In 1882, Ferdinand von Lindenmann proved that π is a transcendental number.
- A transcendental number cannot be the root of any polynomial equation with integer coefficients.
- This means you cannot write π as a simple fraction, and you cannot find its exact value by combining whole numbers using basic math or roots.
- Because the side length of the square would be the square root of π, and π is transcendental, the square root of π is also transcendental.
- It is impossible to construct a length that is a transcendental number using only a compass and straightedge. This is why the problem cannot be solved.
History of the Problem
People have been trying to solve the problem of squaring the circle for thousands of years.
- Ancient Greek mathematicians, like Anaxagoras and Hippocrates of Chios, worked on this problem.
- Many people believed it was possible and spent their lives trying to find a solution.
- It became a famous challenge that puzzled mathematicians for centuries.
- Even after it was proven impossible, some people still tried to find a solution, not understanding the mathematical proof.
Images for kids
-
Oronce Finé, Quadratura circuli, 1544
See also
 In Spanish: Cuadratura del círculo para niños
In Spanish: Cuadratura del círculo para niños