Rational number Facts for Kids

A rational number is a type of number that you can write as a fraction. Imagine a number like 1/2, 3/4, or even 5/1. All of these are rational numbers! They are often shown with the symbol 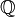$\mathbb{Q}$ , which comes from the word "quotient" (the answer you get when you divide numbers).

Rational numbers are part of a bigger group called real numbers. They can be positive (like 7) or negative (like -2). If a number cannot be written as a simple fraction, it's called an irrational number. Most numbers you use every day, like prices, measurements, or scores, are rational numbers. This includes fractions, whole numbers, and decimals that either stop or repeat.

How to Spot a Rational Number
What Are Irrational Numbers?
Doing Math with Rational Numbers
Related pages
See also

How to Spot a Rational Number

Rational numbers can appear in different forms. Here's how to recognize them:

Rational Numbers as Fractions

Every rational number can be written as a fraction. A fraction is simply one whole number divided by another, like a/b, where b is not zero.

For example, the number 1.5 can be written as:

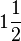$1 \frac{1}{2}$ (a mixed number)
$\frac{3}{2}$ (an improper fraction)
3/2 (another way to write it)

Other examples of fractions that are rational numbers include 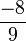$\frac{1}{7}$ , $\frac{-8}{9}$ , and $\frac{2}{5}$ .

Rational Numbers as "Stopping" Decimals

A "stopping" decimal (also called a terminating decimal) is a decimal that has a limited number of digits after the decimal point. It doesn't go on forever.

For instance, 3.2 is a rational number because it stops. You can write it as 32/10. Other examples are 4.075 (which is 4075/1000) and -300.12002. Even a very long decimal like 0.9582938472938498234 is rational because it eventually ends.

Rational Numbers as "Repeating" Decimals

A repeating decimal is a decimal where digits after the decimal point go on forever, but they follow a repeating pattern.

Take the fraction $\frac{1}{3}$ . As a decimal, it's 0.3333333333... The dots mean the digit 3 repeats without end.

Sometimes, a group of digits repeats. For example, 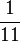$\frac{1}{11}$ is 0.09090909... Here, the group of digits 09 repeats.

It's also possible for the repeating part to start after some other digits. For instance, $\frac{1}{6}$ is 0.16666666... In this case, the digit 6 repeats after the digit 1.

Sometimes, your calculator might make a small rounding error. For example, it might show 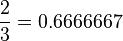$\frac{2}{3} = 0.6666667$ . This is just the calculator rounding the last digit up, even though the 6s should repeat forever.

What Are Irrational Numbers?

Irrational numbers are numbers whose decimal digits never repeat in a pattern and never end. They go on forever without any repeating sequence.

A famous example is π (Pi). Its first few digits are 3.1415926535... No matter how far you calculate, you will never find a repeating pattern in its digits.

Doing Math with Rational Numbers

Rational numbers are very useful because they behave nicely when you do math with them:

If you add or subtract two rational numbers, your answer will always be another rational number.
If you multiply two rational numbers, you will always get another rational number.
If you divide two rational numbers, you will always get another rational number. The only exception is that you cannot divide by zero.
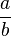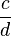Two rational numbers, like $\frac{a}{b}$ and $\frac{c}{d}$ , are equal if 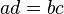Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): ad = bc . This is like cross-multiplying to check if two fractions are the same.

Rational number facts for kids

Contents