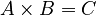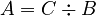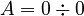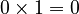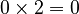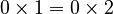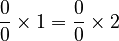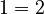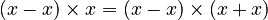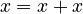Division by zero Facts for Kids

In mathematics, you learn about adding, subtracting, multiplying, and dividing numbers. But there's one special rule: you can never divide a number by zero. It's like a forbidden move in a game! If you try, the answer just doesn't make sense.

Why Can't You Divide by Zero?
Tricky Math Problems Using Division by Zero
- Hiding the Zero
Calculus and Indeterminate Forms
Division by Zero in Computers
Division by Zero in Geometry
Images for kids
See also

Why Can't You Divide by Zero?

Let's think about multiplication first. If you have a number, let's call it A, and you multiply it by another number, B, you get a result, C.

$A \times B = C$

Now, if you want to find A, you would usually divide C by B.

$A = C \div B$

But what if B is zero?

If 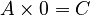$A \times 0 = C$ , then C must always be zero. This is true for any number A.

So, if we try to write this as a division:

$A = 0 \div 0$

The problem is that A could be any number. It could be 1, or 1,000,000,000. Because 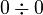$0 \div 0$ doesn't give a single clear answer, we say it is "indeterminate." This means it has no specific value.

What if you try to divide a number that is not zero by zero? For example, 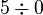$5 \div 0$ .

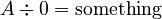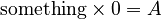If $A \div 0 = \text{something}$ , then $\text{something} \times 0 = A$ .
But we know that anything multiplied by zero is zero. So, 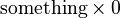$\text{something} \times 0$ will always be zero, not A (unless A is also zero).
Because there's no number that can make this work, we say that dividing a non-zero number by zero is "undefined." Sometimes, people say it leads to infinity, which itself is not a specific number.

Normally, if two things are equal to the same value, they are equal to each other. But this rule doesn't work when that value is 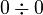$0 \div 0$ . This shows that the usual rules of math break down when you try to divide by zero.

Tricky Math Problems Using Division by Zero

Sometimes, people try to trick you with math problems that secretly use division by zero. This can lead to wrong answers, like proving that 1 equals 2!

Let's look at an example: Imagine we know these are true:

$0 \times 1 = 0$
$0 \times 2 = 0$

Since both are equal to 0, we can say:

$0 \times 1 = 0 \times 2$

Now, if someone tries to divide both sides by zero, they might write:

$\frac{0}{0} \times 1 = \frac{0}{0} \times 2$

If they then incorrectly assume that $\frac{0}{0}$ is equal to 1, they would simplify it to:

$1 = 2$

This "proof" is wrong because you cannot divide by zero and assume $\frac{0}{0}$ is 1. That's the trick!

Hiding the Zero

It's even harder to spot the mistake when the zero is hidden. For example, let's say x is any number. We know that any number minus itself is zero, so 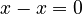$x - x = 0$ . Look at these steps:

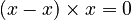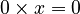$(x - x) \times x = 0$ (because $0 \times x = 0$ )
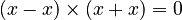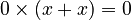$(x - x) \times (x + x) = 0$ (because $0 \times (x+x) = 0$ )

Since both are equal to 0, we can say:

$(x - x) \times x = (x - x) \times (x + x)$

Now, if someone tries to divide both sides by 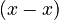$(x - x)$ , they get:

$x = x + x$

Then, if they divide both sides by x:

$1 = 2$

This "proof" is also wrong! The mistake is dividing by 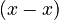$(x - x)$ , because 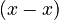$(x - x)$ is actually zero. So, it's another hidden division by zero.

Calculus and Indeterminate Forms

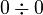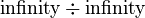In calculus, which is a more advanced part of mathematics, you sometimes deal with "limits." When you try to find the limit of some math problems, you might end up with expressions like $0 \div 0$ or $\text{infinity} \div \text{infinity}$ . These are called "indeterminate forms" because their value isn't immediately clear. You need special methods to figure them out.

Division by Zero in Computers

When a computer program tries to divide a whole number (integer) by zero, the computer's operating system usually stops the program. It will often show an "error message" to the user or programmer. Division by zero is a common mistake, or bug, in computer programming.

If a computer tries to divide floating point numbers (numbers with decimals) by zero, the result is usually either infinity or a special value called "NaN" (which stands for "Not a Number"). This depends on what number was being divided by zero.

Division by Zero in Geometry

In geometry, sometimes the idea of $\frac{1}{0}$ is used to represent infinity. This type of infinity is called "projective infinity." It's different because it's not seen as a positive or negative number, similar to how zero is neither positive nor negative.

Images for kids

Most calculators, such as this Texas Instruments TI-86, will halt execution and display an error message when the user or a running program attempts to divide by zero.
Division by zero on Android 2.2.1's calculator app shows the symbol of infinity.

Division by zero facts for kids

Contents