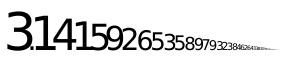Pi facts for kids

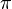This picture shows that pi () is found by dividing a circle's circumference (distance around) by its diameter (distance across).

Pi is a number that goes on forever without repeating.

Pi, also written as 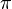, is a special number in math. It helps us understand circles. Imagine you have any circle. If you divide the distance all the way around the circle (called its circumference) by the distance straight across the circle through its center (called its diameter), you will always get the same number. That number is Pi!

Pi starts with 3.14159265... and keeps going forever without any repeating pattern. Numbers like this are called irrational numbers. Even if circles are big or small, the relationship between their circumference and diameter is always the same, so Pi's value never changes.

What is Pi?

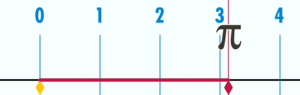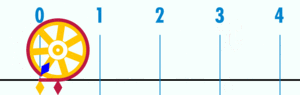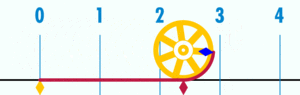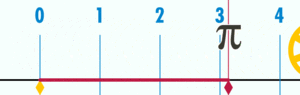
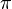This diagram shows how you can find using a circle with a diameter of one. The distance around this circle (its circumference) is exactly .

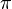Pi is an irrational number. This means you can't write it as a simple fraction like 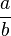, where 'a' and 'b' are whole numbers. The digits of Pi after the decimal point go on forever without repeating in a pattern. Because of this, we can never write down the exact value of Pi. We can only get very close to it.

For everyday use, a good approximation of Pi is 3.14. A common fraction that's close to Pi is 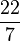, which is about 3.142857. This is usually good enough for most things. If you need a more exact value, 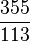is even closer, giving about 3.14159292. Computers can calculate Pi to many, many digits, but we only need a few for most real-life problems.

History of Pi

People have known about Pi for thousands of years. Ancient mathematicians in India, like Bhaskaracharya and Aryabhatt, knew its value. Even very old civilizations like the Babylonians and Egyptians used approximations for Pi around 1900 BC. The Babylonians found that Pi was a little more than 3 by measuring circles with ropes.

The first written record of Pi dates back to 1900 BC. Around 1650 BC, an Egyptian named Ahmes wrote about a value for Pi in a document called the Rhind Papyrus.

Knowledge of Pi eventually reached Europe and the Hebrews. Later, a common way to find Pi was to draw a shape with many sides, called a polygon, inside a circle. By calculating the area of this polygon, mathematicians could get closer to Pi's value.

• The Greek philosopher Archimedes used a polygon with 96 sides to find Pi.
• The Chinese, around 500 A.D., used a polygon with an amazing 16,384 sides!

Since then, many people have tried to find more and more exact values of Pi.

In the 16th century, new ways to find Pi were developed. A French lawyer named François Viète created a complex formula. The Greek symbol "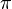" was first used for Pi in an essay by William Jones in 1706.

In 1761, a mathematician named Lambert showed that Pi was an irrational number. This means it cannot be written as a simple fraction. Later, in 1882, another mathematician named Lindeman showed that Pi is also a transcendental number. This means it cannot be the solution to a simple polynomial equation.

Pi is used in many areas of math, not just geometry (the study of shapes). It appears in complex analysis, trigonometry, and mathematical series.

Pi in Real Life

Today, we can calculate Pi to many digits using computers. However, we usually don't need that many for everyday tasks.

Pi is very useful for calculating the area or circumference of any circle.

• To find the circumference (C) of a circle, you use the formula: C = 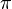times diameter.
• To find the area (A) of a circle, you use the formula: A = 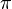times radius squared. This is often written as 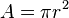, where r is the radius.

Even for very large measurements, you don't need many digits of Pi:

• To find the circumference of a circle with a radius of 30 meters with only a 1 mm error, you need 4 digits of Pi.
• To find the circumference of the Earth with a 1 mm error, you need 10 digits of Pi.
• To find the circumference of a circle the size of the distance from Earth to the Sun with a 1 mm error, you need 15 digits of Pi.

Many people celebrate Pi Day on March 14th. This is because March 14th can be written as 3/14, which matches the first three digits of Pi (3.14).

Images for kids

• 

  Archimedes used polygons to get closer to the value of Pi.

• 

  Isaac Newton

• 

  Srinivasa Ramanujan developed new ways to calculate Pi.

• 

  Pi can even show up in the study of random movements.

• 

  The ancient city of Carthage was said to be founded using a problem that relates to circles.

• 

  An animation of a geodesic in the Heisenberg group.

• 

  Pi is used in understanding spherical harmonics in vector calculus.

• 

  Complex math functions, like the logarithm of the Gamma function, use Pi.

• 

  Pi is connected to prime numbers through Prüfer groups.

• 

  The Cauchy distribution, which involves Pi, describes how particles move randomly.

• 

  The Mandelbrot set, a famous fractal, can be used to approximate Pi.

• 

  A pi pie. Pies are circular, and "pie" sounds like "Pi," making them a fun subject for Pi puns.

See also

In Spanish: Número π para niños