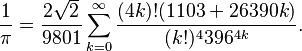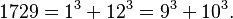Srinivasa Ramanujan facts for kids
Quick facts for kids
Srinivasa Ramanujan
|
|
|---|---|
 |
|
| Born |
Srinivasa Ramanujan Aiyangar
22 December 1887 |
| Died | 26 April 1920 (aged 32) Kumbakonam, Madras, British India
|
| Citizenship | British India |
| Education |
|
| Known for |
|
| Awards | Fellow of the Royal Society (1918) |
| Scientific career | |
| Fields | Mathematics |
| Institutions | Trinity College, Cambridge |
| Thesis | Highly Composite Numbers (1916) |
| Academic advisors | |
| Influences | G. S. Carr |
| Signature | |
Srinivasa Ramanujan (born Srinivasa Ramanujan Aiyangar; 22 December 1887 – 26 April 1920) was a brilliant Indian mathematician. Even though he had very little formal training in advanced mathematics, he made huge contributions to different areas of math. These included mathematical analysis, number theory, infinite series, and continued fractions. He even found solutions to problems that were thought to be impossible to solve at the time.
Ramanujan first worked on his math ideas all by himself. He tried to get leading mathematicians interested in his work. However, many found his ideas too new and presented in unusual ways. In 1913, he started writing letters to an English mathematician named G. H. Hardy at the University of Cambridge. Hardy quickly saw that Ramanujan's work was amazing. He arranged for Ramanujan to come to Cambridge. Hardy noted that Ramanujan had created brand new theorems. Some of them "defeated me completely," he said, meaning he had never seen anything like them before.
During his short life, Ramanujan independently discovered almost 3,900 mathematical results. Many of these were completely new. His unique ideas, like the Ramanujan prime and mock theta functions, opened up entirely new fields of study. They have inspired a lot of research even today. Most of his thousands of results have now been proven correct. The Ramanujan Journal was created to publish math influenced by him. His notebooks, which contain summaries of his work, have been studied for decades. Even as late as 2012, researchers were still finding deep number theory results hidden in his simple notes. He became one of the youngest Fellows of the Royal Society and the first Indian to be elected a Fellow of Trinity College, Cambridge. Hardy compared Ramanujan to other math geniuses like Euler and Jacobi.
In 1919, Ramanujan became very ill. It is now thought he had a liver infection called amoebiasis. This illness made him return to India, where he died in 1920 at just 32 years old. His last letters show he was still creating new math ideas. His "lost notebook", found in 1976, contained discoveries from his last year. It caused great excitement among mathematicians.
Contents
Early Life and Education

Ramanujan was born on 22 December 1887, in Erode, Tamil Nadu, India. His family was Tamil Brahmin. His father, Kuppuswamy Srinivasa Iyengar, worked as a clerk. His mother, Komalatammal, was a housewife and sang at a local temple. They lived in a small home in Kumbakonam, which is now a museum. When he was a baby, Ramanujan survived smallpox.
He started school in 1892. After some family moves, he settled back in Kumbakonam. His mother taught him about Hindu traditions and songs. At Kangayan Primary School, Ramanujan was a good student. In 1897, he passed his primary exams with the best scores in his area. That year, he started at Town Higher Secondary School, where he began to learn formal mathematics.
By age 11, he had already learned more math than two college students living at his home. At 13, he mastered a book on advanced trigonometry and even discovered new theorems on his own. By 14, he was winning awards and helping his school organize its students and teachers. He could finish math exams in half the time. In 1902, he learned to solve cubic equations and later created his own way to solve quartic equations.
In 1903, at 16, Ramanujan found a book called Synopsis of Pure Mathematics by G. S. Carr. This book had 5,000 math theorems. Ramanujan studied it very carefully. The next year, he discovered Bernoulli numbers and calculated the Euler–Mascheroni constant to many decimal places. His classmates often said they didn't understand him but respected his talent.
After graduating in 1904, Ramanujan received a math prize. He got a scholarship to Government Arts College, Kumbakonam. However, he loved math so much that he ignored other subjects and failed them. This caused him to lose his scholarship. He later tried another college, Pachaiyappa's College in Madras. He did well in math but failed other subjects like English. He left college without a degree and continued his math research on his own. He lived in great poverty during this time.
In 1910, Ramanujan met V. Ramaswamy Aiyer, who founded the Indian Mathematical Society. This meeting helped Ramanujan start to get recognition for his math work in Madras. He soon became a researcher at the University of Madras.
Adult Life in India
On 14 July 1909, Ramanujan married Janaki, who was ten years old. It was common at that time for marriages to be arranged with young girls. Janaki stayed with her family for three years after the wedding. In 1912, she moved in with Ramanujan and his mother in Madras.
After his marriage, Ramanujan had a health issue that needed surgery. His family could not afford it, but a doctor volunteered to help him for free in 1910. After recovering, Ramanujan looked for a job. He tutored students and eventually got a temporary job at the Madras Accountant General's office.
In 1912, he applied for a job at the Madras Port Trust. His application included a recommendation from E. W. Middlemast, a math professor. Middlemast wrote that Ramanujan was "a young man of quite exceptional capacity in Mathematics." Ramanujan got the job as an accounting clerk. He finished his work quickly and spent his extra time doing math research. His boss, Francis Spring, and a colleague, S. Narayana Iyer, encouraged his math pursuits.
Reaching Out to British Mathematicians
In 1913, Ramanujan's friends tried to show his work to British mathematicians. Some, like M. J. M. Hill, said Ramanujan's papers had mistakes and that he lacked formal education. However, Hill still gave him serious advice. With help, Ramanujan wrote letters to top mathematicians at Cambridge University.
Two professors, H. F. Baker and E. W. Hobson, sent his papers back without comments. But on 16 January 1913, Ramanujan wrote to G. H. Hardy. At first, Hardy thought the nine pages of math from an unknown person might be a trick. But he soon saw that some of Ramanujan's formulas were amazing and seemed impossible to invent if they weren't true. Hardy showed the papers to his colleague, J. E. Littlewood, who was also very impressed. Hardy concluded that Ramanujan was "a mathematician of the highest quality."
Hardy wrote back to Ramanujan, asking for proofs of his ideas. He also contacted the Indian Office to help Ramanujan travel to Cambridge. However, Ramanujan initially refused to leave India due to his religious beliefs. Meanwhile, he kept sending Hardy more theorems.
Gilbert Walker, a former Cambridge lecturer, also saw Ramanujan's work and urged him to come to Cambridge. Because of this, the University of Madras gave Ramanujan a monthly research scholarship for two years.
Ramanujan continued to publish papers in the Journal of the Indian Mathematical Society. In one paper, he had ideas similar to a Polish mathematician whose work had just arrived. Eventually, Ramanujan changed his mind about going to England. It is said his mother had a dream where her family goddess told her to let her son fulfill his life's purpose. On 17 March 1914, Ramanujan sailed to England, leaving his wife with his parents.
Life in England


Ramanujan arrived in London on 14 April 1914. He was met by E. H. Neville, who took him to Cambridge. Ramanujan quickly started working with Littlewood and Hardy. After six weeks, he moved into his own place, close to Hardy's room.
Hardy and Littlewood began to study Ramanujan's notebooks. Ramanujan had sent 120 theorems in his first letters, but the notebooks had many more. Hardy found that some were wrong, some were already known, but many were completely new and groundbreaking. Both Hardy and Littlewood were deeply impressed. Littlewood said he believed Ramanujan was "at least a Jacobi" (a famous mathematician).
Ramanujan spent almost five years in Cambridge, working with Hardy and Littlewood. They published some of his discoveries. Hardy and Ramanujan had very different personalities and working styles. Hardy believed strongly in strict mathematical proofs, while Ramanujan was very religious and relied on his intuition. Hardy tried to teach Ramanujan how to write formal proofs without stopping his amazing flow of new ideas. This was not easy for either of them.
In March 1916, Ramanujan earned a degree for his work on highly composite numbers. This paper was over 50 pages long and showed his amazing skill with numbers.
On 2 May 1918, Ramanujan was elected a Fellow of the Royal Society, a very high honor for scientists. He was only the second Indian to receive this. At 31, he was one of the youngest Fellows ever. He was recognized for his work on elliptic functions and number theory. On 13 October 1918, he became the first Indian to be elected a Fellow of Trinity College, Cambridge.
Illness and Death
Ramanujan had many health problems throughout his life. His health got worse in England. It was hard for him to follow his strict religious diet there, and wartime food rationing also affected him. He was thought to have tuberculosis and a severe vitamin deficiency. He had to stay in a special hospital. In 1919, he returned to Kumbakonam, India. He died in 1920 at the age of 32.
After his death, his brother collected Ramanujan's remaining notes. These notes contained many formulas. Ramanujan's wife, Janaki Ammal, moved to Mumbai and later back to Madras. She supported herself with a pension and by tailoring clothes. She later adopted a son. In her older years, she received pensions from various organizations. She always honored Ramanujan's memory and worked to make sure his achievements were recognized. She died in 1994.
A study in 1994 suggested that Ramanujan's symptoms were more like those of hepatic amoebiasis, a liver infection common in Madras at the time. He had suffered from dysentery before leaving India. If not treated properly, amoebic dysentery can cause problems years later. At the time, amoebiasis could be treated, and British soldiers with it were being cured around when Ramanujan left England.
Personality and Beliefs
Ramanujan was described as a quiet and shy person, but also dignified and polite. He lived a simple life in Cambridge. His first biographers from India said he was a very strict Hindu. He believed his math abilities came from his family goddess, Namagiri Thayar. He said he would dream of blood drops, which symbolized her husband. Later, he had visions of complex math ideas unfolding before his eyes. He often said, "An equation for me has no meaning unless it expresses a thought of God."
Hardy said that Ramanujan believed all religions were equally true. Hardy also felt that Westerners sometimes made Ramanujan's religious beliefs seem more mystical than they were. However, Hardy did note Ramanujan's strict vegetarian diet.
Another mathematician, Bruce C. Berndt, said that people often wrongly think Ramanujan had magical math powers. He explained that Ramanujan carefully wrote down all his results in his notebooks. Berndt thought Ramanujan probably did his rough work and proofs on a slate because paper was expensive. Then he would write the final results in his notebooks.
Amazing Math Discoveries
In mathematics, there's a difference between having a brilliant idea and proving it. Ramanujan came up with many formulas that mathematicians later studied in detail. G. H. Hardy said Ramanujan's discoveries were incredibly rich and often held more meaning than first appeared. His work opened up new areas of research.
One of Ramanujan's most interesting formulas is an infinite series for π, which helps calculate pi very quickly:
This formula is so fast that it's used in some of the quickest ways to calculate pi today. Even using just the first part of the sum gives a very accurate value for pi.
Ramanujan was also amazing at solving problems quickly. Here's a story:
Imagine you are on a street with houses numbered 1 to n. There is a house in the middle (x) where the sum of house numbers to its left is equal to the sum of house numbers to its right. If n is between 50 and 500, what are n and x? Ramanujan thought about it and gave the answer with a twist. He gave a continued fraction that solved this whole type of problem. The person who asked, P. C. Mahalanobis, was amazed. Ramanujan said, "It is simple. The minute I heard the problem, I knew that the answer was a continued fraction. Which continued fraction, I asked myself. Then the answer came to my mind."
In 1918, Hardy and Ramanujan studied the partition function P(n). This function counts how many ways a number can be broken down into smaller numbers. Their work led to a powerful new method for finding formulas called the circle method.
In his last year, Ramanujan discovered mock theta functions. For many years, these functions were a mystery. Now, we know they are important in advanced mathematics.
Ramanujan's Notebooks
While in Madras, Ramanujan wrote most of his math results in four notebooks. He usually wrote down the final results without showing how he got them. This led some people to think he couldn't prove his work. However, mathematician Bruce C. Berndt believes Ramanujan could prove most of his results but chose not to write down the proofs.
This might be because paper was expensive, so he did his work on a slate and only wrote the final answers on paper. He might also have been influenced by G. S. Carr's book, which also stated results without proofs. It's also possible Ramanujan thought his work was just for himself.
The first notebook has 351 pages, the second has 256 pages, and the third has 33 pages. These notebooks have inspired many mathematicians to prove what Ramanujan had found.
In 1976, a fourth notebook with 87 pages was found. This is known as "Ramanujan's lost notebook."
The Hardy–Ramanujan Number 1729
The number 1729 is famous because of a story about Hardy visiting Ramanujan in the hospital. Hardy said that Ramanujan believed "Every positive integer was one of [Ramanujan's] personal friends."
Hardy came to visit Ramanujan, who was ill in a taxi. Hardy mentioned that the taxi number was 1729, and he thought it was a "dull" number. Ramanujan immediately replied that it was a very interesting number! He said it was the smallest number that can be written as the sum of two cubes in two different ways:
This idea has led to the concept of "taxicab numbers."
How Mathematicians Saw Ramanujan
When asked how Ramanujan came up with his solutions, Hardy said they were "arrived at by a process of mingled argument, intuition, and induction." He added that Ramanujan couldn't fully explain his methods. Hardy also said he had "never met his equal" and could only compare him to Euler or Jacobi. Littlewood said it was hard to teach Ramanujan European mathematics because every new idea he heard would make Ramanujan come up with original ideas, stopping the lesson.
K. Srinivasa Rao shared a story from mathematician Paul Erdős. Erdős said Hardy rated mathematicians on a scale of 0 to 100 for pure talent. Hardy gave himself a 25, Littlewood a 30, David Hilbert an 80, and Ramanujan a 100. This shows how highly Ramanujan was regarded. Bruce C. Berndt said in 2011 that as almost all of Ramanujan's ideas have been proven, his work is now appreciated even more. His work is now used in many areas of modern math and physics.
Honors and Recognition

The year after Ramanujan died, the science journal Nature listed him among important scientists. His home state of Tamil Nadu celebrates 22 December (Ramanujan's birthday) as 'State IT Day'. The government of India has issued stamps with Ramanujan's picture in 1962, 2011, 2012, and 2016.
Since 1987, his birthday, 22 December, has been celebrated as Ramanujan Day at the Government Arts College, Kumbakonam, where he studied. The International Centre for Theoretical Physics (ICTP) has a prize in Ramanujan's name for young mathematicians from developing countries. SASTRA University gives a US$10,000 prize each year to a mathematician under 32 for great work influenced by Ramanujan.
SASTRA University also has the Srinivasa Ramanujan Centre and the House of Ramanujan Mathematics, a museum about his life. SASTRA bought and fixed up the house where Ramanujan lived in Kumbakonam.
In 2011, for his 125th birthday, the Indian government declared 22 December as National Mathematics Day. The Prime Minister also said that 2012 would be the National Mathematics Year.
Ramanujan IT City is a large technology park in Chennai built in 2011. It is named after him to honor his contributions.
Commemorative Postal Stamps
Stamps released by India Post to honor Ramanujan:
Images for kids
- 1729 (number)
- List of Indian mathematicians
- Ramanujan graph
- Ramanujan summation
- Ramanujan's constant
- Ramanujan's ternary quadratic form
- Rank of a partition
See also
 In Spanish: Srinivasa Ramanujan para niños
In Spanish: Srinivasa Ramanujan para niños