Theorem facts for kids

The Pythagorean theorem has at least 370 known proofs.

In mathematics, a theorem is an idea or statement that has been proven to be true. Mathematicians use logic and other facts that are already known to prove theorems. Think of it like building a strong argument where every step is correct.

Sometimes, a smaller idea needs to be proven first to help prove a bigger theorem. This smaller idea is called a lemma. Every theorem usually has two main parts: the starting ideas, called hypotheses, and the final result, called the conclusion.

Theorems are proven using deduction. This means you start with general rules and figure out specific results. This is different from theories in science, which are often based on experiments and observations.

Different Kinds of Theorems

Some theorems are quite simple. Their proof might be very short and easy to understand because they follow directly from basic rules.

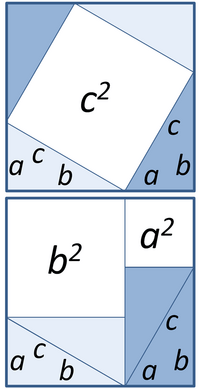
Other theorems are called "deep" theorems. Their proofs are often very long and difficult. These proofs might even connect different areas of mathematics, showing how they are related. A theorem can be simple to say but still be very deep. A great example is Fermat's Last Theorem. There are many other simple-sounding but deep theorems in areas like number theory and combinatorics.

Theorems Proven by Computers

There are also theorems where the proof is known, but it's too big or complex for a person to write down easily. Good examples include the four color theorem and the Kepler conjecture. These theorems were proven by turning them into a huge puzzle that a computer could solve. The computer checked many possibilities to confirm they were true.

At first, some mathematicians weren't sure about this way of proving things. But over time, it has become more accepted. Some mathematicians, like Doron Zeilberger, even believe these might be the only truly complex results mathematicians have ever proven. Many math problems, like trigonometric identities, can be solved by simpler computer calculations.

Related Pages

• Proposition

Images for kids

• 

  The Collatz conjecture is a complex problem. When extended to complex numbers, it creates a fractal pattern similar to the Mandelbrot set.

See also

In Spanish: Teorema para niños