Fractal facts for kids

A Sierpinski triangle, after 7 steps.

The Mandelbrot set is a famous example of a fractal.

A fractal is a special kind of pattern or shape. If you zoom in on a fractal, you'll see the same pattern repeating itself, no matter how close you look! It's like a small part of the shape looks just like the whole shape.

The word fractal was created by a mathematician named Benoît Mandelbrot in 1975. It comes from the Latin word fractus, which means "broken" or "fractured." Think of a tree: a big branch splits into smaller branches, and those smaller branches split into even tinier ones. This is a bit like a fractal! Fractals are not just cool to look at; they also have many real-world uses.

Types of Fractals

There are many different kinds of fractals, and they can be made in various ways. Two famous examples are the Sierpinski triangle and the Mandelbrot set. The Sierpinski triangle is built using repeating patterns. The Mandelbrot set, on the other hand, is created from a mathematical equation.

You can also find fractals all around you in nature! Trees, snowflakes, some vegetables like broccoli, and even coastlines show fractal-like patterns.

The Koch Curve

How to make the Koch Curve

The Koch Curve is a simple example of a fractal. Let's see how it's made:

• Start with a straight line.
• Divide this line into three equal parts.
• Remove the middle part.
• In its place, add two new lines that form the top two sides of an equilateral triangle. Now you have four line segments.
• Repeat these steps for each of the four new line segments.
• Keep doing this forever! The shape you end up with is the Koch Curve.

It's pretty strange, but the Koch Curve has an infinite length, even though it fits into a small area. Its area is actually zero! This is because it's not quite a 1D line and not quite a 2D shape.

What is Fractal Dimension?

Since the Koch Curve has infinite length but zero area, it seems to be somewhere between a 1D line and a 2D shape. Scientists use something called "fractal dimension" to describe how "space-filling" a fractal is. For the Koch Curve, we want a dimension between 1 and 2.

To find the dimension of a simple fractal like the Koch Curve, we can use a formula.

• The Koch Curve can be broken down into 4 smaller pieces. Each of these pieces is 1/3 the size of the original segment.
• We call the number of smaller pieces N (which is 4 for the Koch Curve).
• We call the scaling factor B (which is 1/3 for the Koch Curve).

The formula for the similarity dimension is: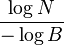

Here, 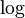is a mathematical function called the logarithm. For the Koch Curve, if you put in the numbers, you get about 1.2619. This number tells us that the Koch Curve is more complex than a simple line (dimension 1) but less complex than a flat surface (dimension 2). For the Koch Curve, this "similarity dimension" is the same as its Hausdorff Dimension, which is a more advanced way to measure fractal dimension.

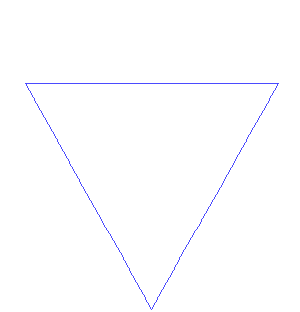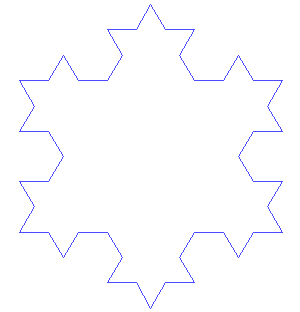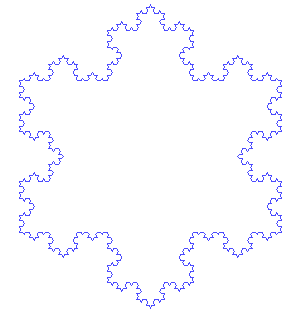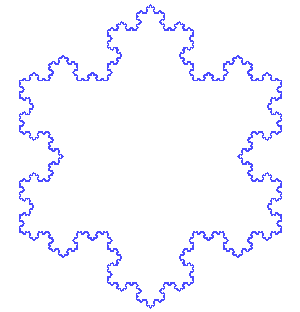
Koch Snowflake

The Koch snowflake starts with a triangle.

The Koch snowflake is very similar to the Koch curve. The only difference is that you start with an equilateral triangle instead of a single straight line. You apply the same steps to each side of the triangle, creating a beautiful, intricate snowflake shape.

How Fractals Are Used

Fractals are not just cool mathematical shapes; they have many practical uses in the real world!

• Biology: Scientists study fractals to understand how our bodies work, like the branching patterns in our lungs, kidneys, and even how our heart rate changes.
• Nature: Fractals help us understand natural events like earthquakes and the shapes of coastlines.
• Technology: Fractals are used to design very efficient radio antennas. They are also used in computer chips to connect all the tiny parts in a very organized way.
• Art: Some fractals are created purely for their beauty and artistic appeal.

Studying fractals helps us understand why these complex, repeating patterns appear so often in nature and in technology.

Images for kids

• 

  Zooming into the boundary of the Mandelbrot set

• 

  A simple fractal tree

• 

  A fractal “tree” to eleven iterations

• 

  3D computer generated fractal

• 

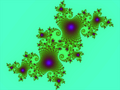
  A Julia set, a fractal related to the Mandelbrot set

• 

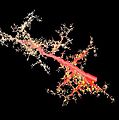
  A Sierpinski gasket can be generated by a fractal tree.

• 

  A strange attractor that exhibits multifractal scaling

• 

  Uniform mass center triangle fractal

• 

  2x 120 degrees recursive IFS

• 

  Self-similar branching pattern modeled in silico using L-systems principles

• 

  A fractal generated by a finite subdivision rule for an alternating link

• 

  A fractal that models the surface of a mountain (animation)

• 

  3D recursive image

• 

  Recursive fractal butterfly image

• 

  A fractal flame

See also

In Spanish: Fractal para niños