Sierpinski triangle facts for kids

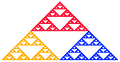
A Sierpinski triangle is a super cool shape called a fractal. Imagine you start with a big triangle. Then, you take out the middle part, leaving three smaller triangles at the corners. Now, you do the exact same thing to each of those three smaller triangles! You keep repeating this process over and over again.

If you keep doing this forever, the Sierpinski triangle becomes a shape with no area, even though it still looks like a triangle! These amazing shapes can also be made in 3D, like a pyramid.

How a Sierpinski triangle grows step by step

What is a Fractal?

A fractal is a shape that looks the same no matter how much you zoom in. It's like a tiny part of the shape is a smaller copy of the whole shape. This idea is called self-similarity. The Sierpinski triangle is a perfect example of a self-similar fractal.

How Do You Make a Sierpinski Triangle?

Making a Sierpinski triangle follows a simple set of rules, repeated many times. This repeating process is called iteration.

Here are the steps:

• Start with a large, solid equilateral triangle. This means all its sides are the same length.
• Find the middle point of each side of the triangle. Connect these three middle points with lines. This will create a smaller, upside-down triangle in the very center.
• Remove this middle upside-down triangle. Now you are left with three smaller equilateral triangles, one at each corner of the original big triangle.
• Now, take each of those three smaller triangles and do the exact same thing again! Find their middle points, draw a new upside-down triangle in their center, and remove it.
• You can keep doing this process again and again, as many times as you like! Each time you repeat the steps, the Sierpinski triangle gets more detailed and complex.

What Happens If You Keep Going Forever?

If you could repeat the steps of making a Sierpinski triangle an infinite number of times, something interesting happens. Even though the shape would still look like a triangle, its total area would become zero! This is because you are always removing more and more space from it. It's a bit mind-bending, but that's the magic of fractals.

Sierpinski in 3D!

Sierpinski shapes aren't just flat! You can also create 3D versions, like a Sierpinski pyramid (also called a Sierpinski tetrahedron). Instead of starting with a flat triangle, you start with a solid pyramid. Then, you remove the middle part, leaving smaller pyramids at the corners. Just like the flat version, you keep repeating this process on the smaller pyramids.

Images for kids

• 

  A Sierpinski pyramid, a 3D version of the fractal

• 

  Generated using a random algorithm

• 

  Animated creation of a Sierpinski triangle using the chaos game

• 

  Animated construction of a Sierpinski triangle

• 

  A Sierpinski Triangle is outlined by a fractal tree with three branches forming an angle of 120° and splitting off at the midpoints. If the angle is reduced, the triangle can be continuously transformed into a fractal resembling a tree.

• 

  Each subtriangle of the nth iteration of the deterministic Sierpinski triangle has an address on a tree with n levels (if n=∞ then the tree is also a fractal); T=top/center, L=left, R=right, and these sequences can represent both the deterministic form and, "a series of moves in the chaos game"

• 

  Sierpinski triangle using an iterated function system

• 

  Animated arrowhead construction of Sierpinski gasket

• 

  Arrowhead construction of the Sierpinski gasket

• 

  Sierpinski pyramid recursion progression (7 steps)

• 

  A Sierpiński triangle-based pyramid as seen from above (4 main sections highlighted). Note the self-similarity in this 2-dimensional projected view, so that the resulting triangle could be a 2D fractal in itself.

See also

In Spanish: Triángulo de Sierpinski para niños