Fermat's Last Theorem facts for kids
Fermat's Last Theorem is a very famous idea in mathematics. It's a special rule about numbers. It says that if you have a whole number n that is bigger than 2 (like 3, 4, 5, and so on), then the equation:
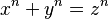
has no solutions if x, y, and z are natural numbers. Natural numbers are positive whole numbers like 1, 2, 3, and so on. This means you can't find any natural numbers x, y, and z that make this equation true when n is a whole number larger than 2.
A mathematician named Pierre de Fermat wrote about this idea in 1637. He wrote it in the margin of his copy of a book called Arithmetica. He claimed he had a proof for it, but said there wasn't enough space to write it down. For 357 years, no one could find a correct proof. It was finally proven in 1995. Most mathematicians today believe that Fermat probably didn't have a complete proof after all.
What is Fermat's Last Theorem?
Fermat's Last Theorem is like a more general version of another famous equation: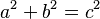 
. This equation comes from the Pythagorean theorem, which you might know from geometry. It describes the sides of a right-angled triangle.
When a, b, and c are whole numbers in the Pythagorean equation, they are called a "Pythagorean triple." For example, 3, 4, and 5 form a triple because 3^2 + 4^2 = 5^2 (which is 9 + 16 = 25). Another example is 5, 12, and 13, because 5^2 + 12^2 = 13^2 (which is 25 + 144 = 169). There are an infinite number of these Pythagorean triples.
Fermat's Last Theorem asks what happens if you change the '2' in the equation 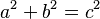to a bigger whole number, like 3, 4, or 5. It states that if n is any whole number greater than 2, then you cannot find any natural numbers x, y, and z that solve the equation .
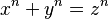The Long Search for a Proof
Over many years, mathematicians found proofs for some specific values of n. For example, Euler proved it for n=3, and Fermat himself proved it for n=4. Other mathematicians like Sophie Germain also made progress for certain cases.
However, the real challenge was to prove that the equation has no solution for all whole numbers n greater than 2. This full proof was incredibly hard to find. It took a very long time to solve Fermat's Last Theorem.
An English mathematician named Andrew Wiles finally found a complete solution in 1995. This was 358 years after Fermat first wrote his note! Another mathematician, Richard Taylor, helped him with the proof. Wiles worked on this problem for eight years.
He proved the theorem by first proving something called the modularity theorem (which was known as the Taniyama–Shimura conjecture at the time). Then, using another idea called Ribet's Theorem, he was able to show that Fermat's Last Theorem must be true. For his amazing work, he received the Wolfskehl Prize in 1997, which was worth about $50,000.
After a few years of debate and checking, mathematicians around the world agreed that Andrew Wiles had indeed solved the problem. Wiles used a lot of very advanced and modern mathematics, and he even created some new math ideas himself. This kind of mathematics didn't exist when Fermat was alive. This is why most people believe that Fermat couldn't have had a complete proof of the theorem himself.
Images for kids
-
Problem II.8 in the 1621 edition of the Arithmetica of Diophantus. On the right is the margin that was too small to contain Fermat's alleged proof of his "last theorem".
-
Fermat's infinite descent for Fermat's Last Theorem case n=4 in the 1670 edition of the Arithmetica of Diophantus (pp. 338–339).
-
Ukrainian copyright certificate for a "proof" of Fermat's Last Theorem
See also
In Spanish: Último teorema de Fermat para niños
