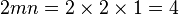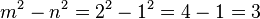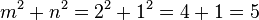Pythagorean theorem Facts for Kids

The Pythagorean theorem shows how the sides of a right triangle are related.

The Pythagorean theorem is a super important rule in mathematics that talks about the sides of a special kind of triangle called a right triangle.

A right triangle always has one angle that measures exactly 90 degrees. This is called the right angle. The two sides that touch the right angle are called the legs. The side across from the right angle is called the hypotenuse. The hypotenuse is always the longest side of a right triangle.

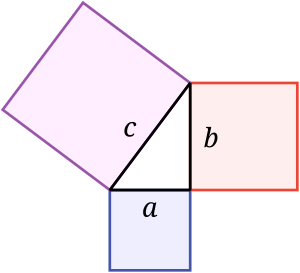
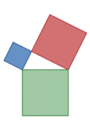
The Pythagorean theorem says that if you make a square on each side of a right triangle, the area of the square on the hypotenuse is equal to the sum of the areas of the squares on the two legs. Imagine the picture: the area of the blue square plus the area of the red square equals the area of the purple square! This amazing rule is named after the Greek mathematician Pythagoras.

If we call the lengths of the legs a and b, and the length of the hypotenuse c, then the theorem can be written as: 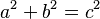$a^2+b^2=c^2$

This means "a squared plus b squared equals c squared." There are many different ways to prove this theorem, showing how it always works!

Understanding the Proof
- Proof Using Similar Triangles
Pythagorean Triples
Images for kids
See also

Understanding the Proof

This diagram helps explain one way to prove the Pythagorean theorem.

Mathematicians have found many ways to prove the Pythagorean theorem. One famous proof was discovered by a Greek mathematician named Eudoxus of Cnidus.

This proof uses a few simple ideas:

Triangles that have the same base and the same height will always have the same area.
A triangle that has the same base and height as one side of a square will have half the area of that square.
If two triangles have two sides and the angle between those sides that are the same, then the triangles are congruent (exactly the same shape and size) and have the same area.

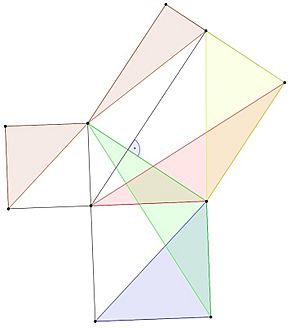
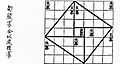
Here's a simplified way to think about the proof using the image:

The blue triangle and the green triangle have the same area. This is because they share the same base and height (using the first idea above).
The green triangle and the red triangle are congruent, so they have the same area. This is because they have two sides and the angle between them that are equal (using the third idea).
The red triangle and the yellow triangle have the same area because they have the same base and height (using the first idea again).
So, the areas of the blue, green, red, and yellow triangles are all equal!
The brown triangles also have the same area for similar reasons.
Each blue triangle and each brown triangle represents half the area of one of the smaller squares built on the legs.
When you add the areas of these halves together, you get half the area of the bigger square (the one on the hypotenuse). Since the halves are equal, the full areas of the small squares added together must equal the full area of the big square!

Proof Using Similar Triangles

This diagram shows how similar triangles can prove the theorem.

Another cool way to prove the Pythagorean theorem uses the idea of similar triangles. Similar triangles are triangles that have the same shape but can be different sizes. Their angles are the same, and their sides are in proportion.

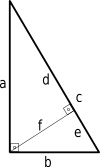
Imagine a right triangle. If you draw a line from the right angle straight down to the hypotenuse, it creates two smaller triangles. These two smaller triangles are similar to the original big triangle, and they are also similar to each other!

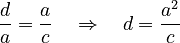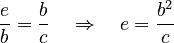
Using the relationships between the sides of these similar triangles, we can set up equations: Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{d}{a} = \frac{a}{c} \quad \Rightarrow \quad d = \frac{a^2}{c} And: Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{e}{b} = \frac{b}{c} \quad \Rightarrow \quad e = \frac{b^2}{c}

From the picture, we can see that the whole hypotenuse c is made up of d plus e. So, 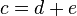$c = d + e \,\!$ . Now, we can replace d and e with the expressions we found: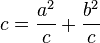 $c = \frac{a^2}{c} + \frac{b^2}{c}$

If we multiply both sides of this equation by c, we get: 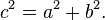$c^2 = a^2 + b^2 \,\!.$ And there you have it – the Pythagorean theorem!

Pythagorean Triples

Pythagorean triples are sets of three whole numbers that fit the equation 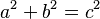$a^2+b^2=c^2$ . These numbers can be the side lengths of a right triangle.

A very famous example is the triangle with sides of 3, 4, and 5. If a=3 and b=4, then: 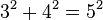$3^2+4^2=5^2$ Because 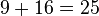$9+16=25$ . This also means that if you take the square root of (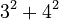Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 3^2+4^2 ), you get 5: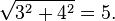 $\sqrt{3^2+4^2}=5.$

The 3-4-5 triangle is special because any set of numbers that are multiples of 3, 4, and 5 will also be Pythagorean triples. For example, 6, 8, and 10 (which is 2 times 3, 4, and 5) also form a right triangle. So do 30, 40, and 50! Another example of a triple is 5, 12, and 13, because 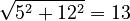Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \sqrt{5^2+12^2}=13 .

A primitive Pythagorean triple is a set of three numbers that are not multiples of any other smaller Pythagorean triple. For example, (3, 4, 5) is primitive, but (6, 8, 10) is not because it's just (3, 4, 5) multiplied by 2.

You can find any primitive Pythagorean triple using a special formula: 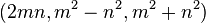$(2mn,m^2-n^2,m^2+n^2)$ . But you need to follow some rules for the numbers m and n:

m and n must be positive whole numbers.
m and n should not have any common factors other than 1.
One of m or n must be even, and the other must be odd (this is called having "opposite parity").
m must be greater than n ( $m>n$ ).

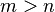If all these rules are met, then m and n will create a primitive Pythagorean triple.

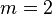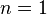Let's try an example: if $m=2$ and $n=1$ . These values follow all four rules.

Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 2mn = 2 \times 2 \times 1 = 4
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): m^2-n^2 = 2^2-1^2 = 4-1 = 3
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): m^2+n^2 = 2^2+1^2 = 4+1 = 5

So, this gives us the primitive triple (3, 4, 5)!