Eudoxus of Cnidus facts for kids
Quick facts for kids
Eudoxus of Cnidus
|
|
|---|---|
| Born | c. 400 BC |
| Died | c. 350 BC Knidos, Asia Minor
|
| Known for | Kampyle of Eudoxus Concentric spheres |
| Scientific career | |
| Fields | |
Eudoxus of Cnidus (born around 408 BC, died around 355 BC) was an important ancient Greek astronomer, mathematician, and scholar. He studied with famous thinkers like Archytas and Plato. Sadly, none of his original writings have survived, but we know about his ideas from other ancient writers.
Contents
Life of Eudoxus
Eudoxus was born and passed away in Cnidus, a city on the southwest coast of Asia Minor (which is now part of Turkey). His name, Eudoxus, means "honored" or "of good reputation" in Greek.
Early Studies and Travels
Eudoxus's father, Aeschines, loved watching the stars. Eudoxus first traveled to Taranto to study mathematics with Archytas. While in Italy, he also visited Sicily to learn medicine from Philiston.
At 23, Eudoxus went to Athens to study with followers of Socrates and attended lectures by Plato. He was quite poor and had to walk about 7 miles (11 km) each day to attend Plato's classes. His friends helped him raise money to travel to Heliopolis, Egypt, where he spent 16 months studying astronomy and mathematics. After Egypt, he traveled north to Cyzicus and then south to the court of Mausolus, gathering many students along the way.
Return to Cnidus
Around 368 BC, Eudoxus returned to Athens with his students. Some sources say he even taught Aristotle. Eventually, he went back to his hometown of Cnidus. There, he became part of the city assembly and built an observatory. He continued to write and teach about theology, astronomy, and meteorology. Eudoxus had one son, Aristagoras, and three daughters: Actis, Philtis, and Delphis.
Eudoxus's Legacy
Eudoxus is famous in mathematical astronomy for introducing the idea of concentric spheres. This helped explain how planets move. His work on proportions was also very important. It helped scientists deal with continuous quantities, not just whole numbers.
Today, there are craters on Mars and the Moon named after him. An algebraic curve called the Kampyle of Eudoxus also carries his name.
Eudoxus's Mathematics
Many consider Eudoxus to be one of the greatest Greek mathematicians, second only to Archimedes in all of Ancient Greece.
Method of Exhaustion
Eudoxus developed a clever technique called the method of exhaustion. This method was a very early version of what we now call integral calculus. It was used to find the areas and volumes of complex shapes. Using this method, Eudoxus proved many important mathematical ideas, such as:
- The areas of circles relate to each other based on the squares of their sizes (radii).
- The volumes of spheres relate to each other based on the cubes of their sizes (radii).
- The volume of a pyramid is one-third the volume of a prism with the same base and height.
- The volume of a cone is one-third the volume of a cylinder with the same base and height.
Understanding Quantities
Eudoxus introduced the idea of mathematical magnitudes to work with continuous shapes like lines, angles, areas, and volumes. This was important because it helped avoid problems with irrational numbers. Before Eudoxus, some mathematicians, like the Pythagoreans, believed that only whole numbers could be used for proofs.
The Pythagoreans had discovered that the diagonal of a square couldn't be measured perfectly with the same unit as its sides. This meant that numbers like the square root of 2 couldn't be written as a simple fraction. This discovery made people question how to measure and calculate in geometry.
Eudoxus found a way to compare quantities without needing exact numbers. This helped restore confidence in using proportions in mathematics. His definition of proportion is a key part of Euclid's famous book, Elements.
Eudoxus's Astronomy
In ancient Greece, astronomy was seen as a part of mathematics. Astronomers tried to create geometric models to show how celestial bodies appeared to move.
Eudoxus's Planetary Models
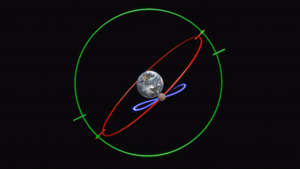
One of Eudoxus's most famous contributions was his model of Concentric spheres. This model tried to explain the movements of the Sun, Moon, and planets using a series of connected spheres, all centered around the Earth.
- The Moon: Eudoxus used three spheres for the Moon.
- The first sphere rotated once every 24 hours, explaining why the Moon rises and sets.
- The second sphere rotated once a month, showing the Moon's journey through the zodiac.
- The third sphere also rotated monthly but was tilted slightly. This explained why the Moon sometimes moved above or below its usual path.
- The Sun: The Sun also had three spheres, similar to the Moon's, but the second sphere completed its motion in a year instead of a month.
- The Planets: The five visible planets (Mercury, Venus, Mars, Jupiter, and Saturn) each had four spheres.
- The first sphere explained their daily rising and setting.
- The second sphere showed their movement through the zodiac.
- The third and fourth spheres worked together to explain retrograde motion. This is when a planet seems to slow down, move backward for a bit, and then move forward again. By tilting these two spheres and rotating them in opposite directions at the same speed, Eudoxus could make a point on the inner sphere trace a figure-eight shape, called a hippopede.
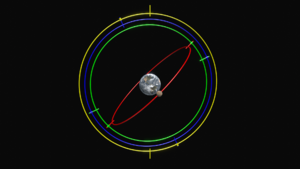
Importance of Eudoxus's System
Later, another Greek astronomer named Callippus added more spheres to Eudoxus's original 27. Even Aristotle described these systems.
However, Eudoxus's system had a main problem: it couldn't explain why the brightness of planets changes when seen from Earth. Since all the spheres were centered on Earth, the planets would always stay the same distance away. Later astronomers came up with new models to fix this. Still, Eudoxus's work was very important for the development of Greek astronomy.
Eudoxus's Ideas on Ethics
Aristotle, in his book Nicomachean Ethics, mentions Eudoxus's ideas about hedonism. Hedonism is the belief that pleasure is the main goal or "good" that all activities aim for.
According to Aristotle, Eudoxus argued for this idea with these points:
- Everything, whether it can think or not, tries to achieve pleasure. Things aim for what they believe is good, and what most things aim for is a good sign of what the main good is.
- Also, the opposite of pleasure, which is pain, is avoided by everyone. This further supports the idea that pleasure is seen as good by all.
- People don't look for pleasure as a way to get something else; they seek it as a goal in itself.
- Any other good thing you can imagine would be even better if pleasure were added to it. Eudoxus believed that only good things can make other good things better.
- Among all good things, happiness is special because it isn't praised in the same way other good things are. This might show that happiness is the highest good of all.
See also
 In Spanish: Eudoxo de Cnido para niños
In Spanish: Eudoxo de Cnido para niños
- Euclid
- Euclid's Elements
- Eudoxus reals
- Delian problem
- Incommensurable magnitudes
- Speusippus